Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 11

3. Внешней нагрузкой для силового расчета кривошипа 1 (рис. 3.1,г) будет R₂₁ – реакция в шарнире А₁ со стороны 2-го звена на 1-е, найденная на предыдущем шаге. Решением уравнений равновесия кривошипа  определяем  реакции  в  его  опоре  О.

3.3. Внешние  силы

Расчет внешних сил во многих случаях является отдельной задачей, относящейся к специальным наукам. Например, на рис. 3.1,а изображен механизм пресса. Технологическая сила, приложенная к пуансону во время выполнения операции штамповки, вытяжки и т.п. зависит от многих факторов: материала заготовки, скорости процесса, площади обработки и т.д. Расчет такого рода сил изучается в механике сплошной среды. Для всех машин технологические нагрузки вычисляются с помощью соответствующих математических моделей тех процессов, для выполнения которых машина предназначена, поэтому здесь и при выполнении курсового проекта мы  будем  полагать  технологическую  силу  заданной.

По графику, имеющемуся в техническом задании определяете значение F_Т в расчетном положении.

Силы  тяжести  вычисляются  по  известной  формуле

G_i =  m_i g , где:  m_i –  масса  i-го звена,  g – ускорение  свободного  падения.

Инерционная нагрузка для звеньев механизмов в общем случае  состоит  из  двух  компонент.  Сил  инерции:

где:  a_Si – ускорение  центра  масс  i-го  звена,

и  инерционных  моментов; для плоских механизмов:

где:  J_Si – момент  инерции  i-го  звена,  e_i  – его  угловое  ускорение.

Знак минус указывает на то, что инерционная нагрузка направлена противоположно  ускорению.

При выполении силового расчета в курсовом проекте силами трения можно пренебречь.

После вычисления сил инерции и тяжести их следует проанализировать. В курсовом проекте примем следующий критерий: те силы, которые более чем в 30 раз меньше технологической силы будем считать пренебрежимо малыми.

3.3.1. Силовой расчет структурных групп

Структурная  группа типа "шатун – ползун"

Расчет этой группы в курсовом проекте произведем аналитическим методом. Расчетная схема представлена на  рис. 3.5. Реакции в направляющих ползуна зависят от его конструкции. В данном случае реакции перемещаются по направляющим вместе с ползуном. Рабочие длины l₁, l₂  (см. рис. 3.5) являются конструктивными параметрами. Вы их задаете сами.

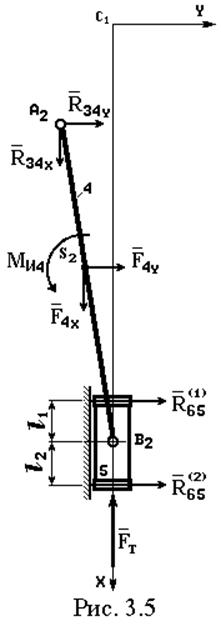Решение удобно получить в НСК OXY, ось X которой параллельна оси ползуна, а начало координат поместим в центр опоры C₁. Уравнение равновесия структурной группы в целом в виде равенства нулю  суммы  всех  сил,  на  нее  действующих:

или в проекциях на оси OXY:

R_34x + F_4x– F_T = 0  ;

R_34y + F_4y + R₆₅⁽¹⁾ + R₆₅⁽²⁾  = 0 .

Из первого уравнения сразу определяется составляющая R_34x. Равновесие шатуна 4 в виде равенства нулю суммы моментов  всех  сил  относительно  точки  В₂:

–R_34x (y_A  – y_B) + R_34y (x_A  – x_B) – F_4x (y_S2  – y_B) + M_И4 +  + F_4y (x_S2  – x_B) = 0.                        ( 3.9 )

Отсюда находим R_34y. Тогда полная реакция в шарнире A₂:

Её направление определяется графически.

Для определения реакций R₆₅⁽¹⁾, R₆₅⁽²⁾ составим систему уравнений, первое из которых отражает равновесие ползуна 5 в виде равенства нулю суммы проекций всех сил на ось Y, а второе – равенство нулю суммы моментов  всех  сил относительно  точки  В:

 R₆₅⁽¹⁾ + R₆₅⁽²⁾  = 0;

–R₆₅⁽¹⁾ l₁ + R₆₅⁽²⁾ l₂ – F_Т (y_S3  – y_B) = 0 .

Решая систему (3.10) найдем реакции R₆₅⁽¹⁾, R₆₅⁽²⁾.

Трехшарнирная структурная  группа

Расчет этой группы в курсовом проекте произведем графоаналитическим методом планов сил.

Рассмотрим случай, характерный для курсовых проектов, когда силы тяжести и инерции пренебрежимо малы по сравнению с усилием R₄₃. Расчетная схема представлена на  рис. 3.6,а. Реакция R₃₄ была найдена при расчете предыдущей структурной группы и .

Назовем нормальным – направление вдоль оси звена, касательным – перпендикулярно оси. На рис. 3.6,а показаны нормальные n₂, n₃ и касательные t₂, t₃ направления для звеньев 2 и 3. Реакции в шарнире A₁ – R₁₂ и в шарнире C₁ – R₆₃, неизвестные как по величине, так и по направлению, будем искать в проекциях на эти направления.