На рис. 4.2 показан график перемещения толкателя для простейшего случая – двухпозиционного механизма, когда весь процесс работы представляется комбинацией четырех ваз: удаление, дальний выстой, возврат и ближний выстой.
4.4. Выбор закона движения выходного звена
Методика выбора закона движения выходного звена зависит от назначения механизма. Как уже отмечалось, по назначению кулачковые механизмы подразделяют на две категории: позиционные и функциональные.
 |
4.4.1. Позиционные механизмы
 Для наглядности рассмотрим самый простой случай двухпозиционного механизма,
который просто “перебрасывает” выходное звено из одного крайнего положения в
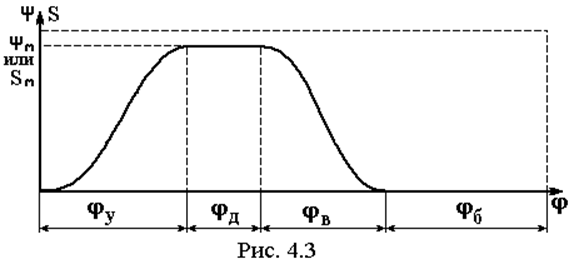
другое и обратно. Закон его перемещения имеет вид, представленный на рис. 4.3,
где j – угол поворота
кулачка, а по оси ординат отложено перемещение выходного звена: для механизмов
с коромыслом y – угол его поворота, для механизмов с толкателем S –
перемещение толкателя. Закон перемещения имеет четыре фазы: удаление, дальний
выстой, возврат и ближний выстой. Соответствующие фазовые углы обозначены: jу, jд, jв, jб.
Для наглядности рассмотрим самый простой случай двухпозиционного механизма,
который просто “перебрасывает” выходное звено из одного крайнего положения в
другое и обратно. Закон его перемещения имеет вид, представленный на рис. 4.3,
где j – угол поворота
кулачка, а по оси ординат отложено перемещение выходного звена: для механизмов
с коромыслом y – угол его поворота, для механизмов с толкателем S –
перемещение толкателя. Закон перемещения имеет четыре фазы: удаление, дальний
выстой, возврат и ближний выстой. Соответствующие фазовые углы обозначены: jу, jд, jв, jб.
В данном случае выбор закона движения состоит в определении характера движения выходного звена на фазах удаления и возврата. На рис. 4.3 для этих участков изображена какая то кривая, но именно ее и надо определить. Какие же критерии закладываются в основу решения этой задачи ?
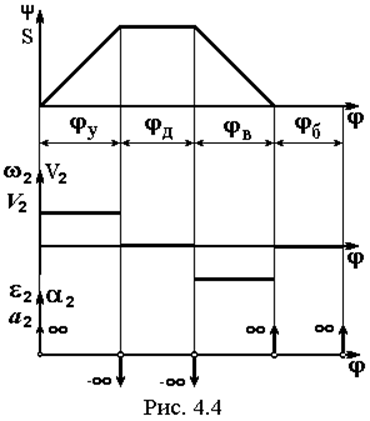
Пойдем от противного. Попробуем поступить “просто”. Зададим на участках удаления и возврата линейный закон перемещения. На рис. 4.4 показано к чему это приведет. Дважды дифференцируя функцию y(j) или S(j) получаем, что на границах фаз будут возникать теоретически бесконечные, т.е. непредсказуемые ускорения, а, следовательно, и инерционные нагрузки. Это недопустимое явление получило название жесткого фазового удара.
 Во избежание этого явления выбор закона движения производят исходя из
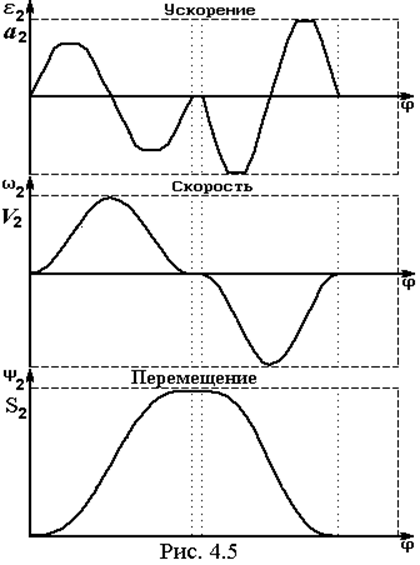
графика ускорения выходного звена. На рис. 4.5 приведен пример. Задаются
желаемой формой графика ускорения и его интегрированием находят функции
скорости и перемещения.
Во избежание этого явления выбор закона движения производят исходя из
графика ускорения выходного звена. На рис. 4.5 приведен пример. Задаются
желаемой формой графика ускорения и его интегрированием находят функции
скорости и перемещения.
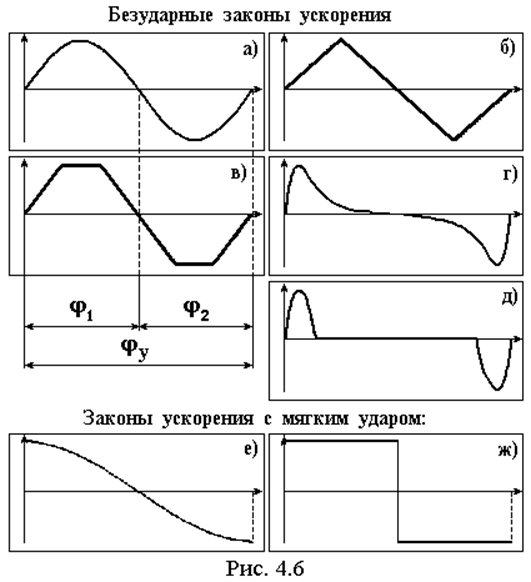
Зависимость ускорения выходного звена на фазах удаления и возврата обычно выбирают безударной, т.е. в виде непрерывной функции без скачков ускорения. Но иногда для тихоходных механизмов с целью уменьшения габаритов допускают явление мягкого удара, когда на графике ускорения наблюдаются скачки, но на конечную, предсказуемую величину.
На рис. 4.6 представлены примеры наиболее часто примеряемых видов законов изменения ускорения. Функции изображены для фазы удаления, на фазе возврата они аналогичны, но зеркально отражены. На рис. 4.6 представлены симметричные законы, когда j1 = j2 и характер кривых на этих участках одинаков. При необходимости применяют и несимметричные законы, когда j1 ¹ j2 или характер кривых на этих участках различен или и то и другое.
Выбор конкретного вида зависит от условий работы механизма, например, закон 4.6д применяют когда на фазе удаления (возврата) нужен участок с постоянной скоростью выходного звена.
Как правило, функции законов ускорения имеют аналитические выражения, в частности 4.6,а,д – отрезки синусоиды, 4.6,б,в,ж – отрезки прямых, 4.6,е – косинусоида, поэтому их интегрирование с целью получения скорости и перемещения не представляет трудностей. Однако заранее не известны амплитудные значения ускорения, но значение перемещения выходного звена на фазах удаления и возврата известны. Рассмотрим как при этом найти и амплитуду ускорения и все функции, характеризующие движение выходного звена.
При постоянной угловой скорости вращения кулачка, когда угол его поворота и время связаны выражением j = wt функции можно рассматривать как от времени, так и от угла поворота. Будем рассматривать их во времени и применительно к механизму с коромыслом.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.