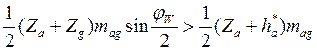Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 31

На рис. 5.18а представлена расчетная схема, где сателлиты занимают предельное положение, когда их окружности выступов уже касаются друг друга. По построению условие существования зазора:

Откуда, учитывая, что угол между осями сателлитов: j_W = 2p/n _W, получаем:

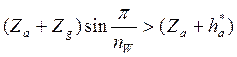
( 5.27 )

Условие сборки. Это условие накладывает ограничение на сочетание чисел зубьев колес так, чтобы, во-первых, обеспечить собираемость механизма, т.е. все зубья сателлитов должны точно входить во впадины ответных колес. А во-вторых, должен существовать период, через который в точности повторяются все фазы зацепления, что увеличивает долговечность передачи.

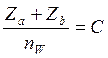Для схемы A это условие выражается как:

( 5.28 )

где C – любое целое число.

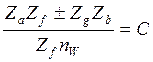Для схем B и C для упрощения сборки обычно назначают числа зубьев центральных колес кратными n_W. Однако есть и более мягкие условия.

Для схем B и C:

( 5.29 )

где знак + берется для схем с разноименными зацеплениями, в частности для схемы B, знак “–” – для схем с одноименными зацеплениями, в частности схемы C.

Условие ( 5.29 ), полученное В.В. Добровольским и предполагающее наиболее простую технологию сборки иногда (хотя и редко) дает отрицательный результат для механизмов, которые могут быть собраны. Известны и другие, например, условие Меррита:

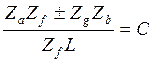
( 5.30 )

где L – наибольший общий делитель чисел Z_g и Z_f.

Однако, при использовании условия  ( 5.30 ) нужно дополнительно рассчитывать, какие конкретно зубья сателлитов с какими впадинами центральных колес должны зацепляться.

Для механизмов схем B и C с двухвенцовыми сателлитами описанные условия сборки необходимо выполнять, когда сателлиты изготавливаются цельными (рис. 5.18б) или венцы жестко фиксируются в одном блоке при сборке. Иногда, особенно в приборных конструкциях делается штифтовое крепление венцов (рис. 5.18в). В этом случае при сборке венцы поворачивают друг относительно друга, подбирая необходимое положение. В этом случае при подборе чисел зубьев условия сборки можно не соблюдать.

5.8.4. Волновые зубчатые механизмы

Волновыми называются механизмы, в составе есть которых упруго деформируемые колеса. По структуре эти механизмы можно отнести к планетарным. Приведем основные термины.

Колесо, которое в процессе работы упруго деформируется – называется гибким колесом.

Колесо, которое в процессе работы не деформируется – называется жестким.

Звено, деформирующее гибкое колесо и с точки зрения структуры являющееся водилом здесь называется генератором волн деформации или просто генератором.

Существует две схемы волновых механизмов:

а) С неподвижным гибким колесом.

б) С неподвижным жестким колесом.

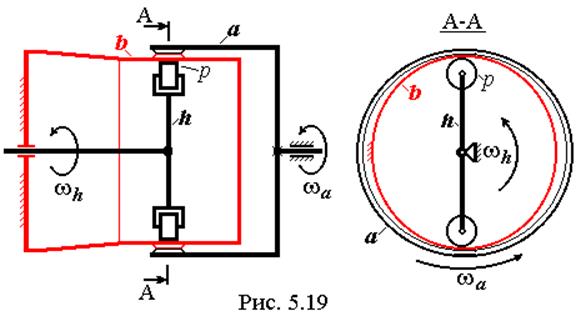
Рассмотрим схему с неподвижным гибким колесом, как более распространенную. Структурная схема такого механизма представлена на рис. 5.19, где а – жесткое колесо, b – гибкое колесо, h – генератор волн, р – ролики.

Входным звеном в этих механизмах является генератор волн (h). Т.к. внешний диаметр генератора делается несколько большим, чем внутренний диаметр гибкого колеса, то генератор, с усилием вставленный внутрь колеса b, деформирует его. При его вращении генератора – вращается деформация гибкого колеса, а т.к. число зубьев колеса b (Z_b) делается на 1 … 3 зуба меньше, чем Z_a, то за каждый оборот генератора происходит разворот колеса а относительно колеса b. Например, если Z_a – Z_b = 1, то за полный оборот генератора h колесо а разворачивается относительно колеса b на угол, соответствующий шагу зацепления.

Найдем передаточное отношение механизма. После остановки водила в данном случае получаем зубчатую пару внутреннего зацепления.

Поскольку по структуре это планетарные механизмы, то можно воспользоваться формулой ( 5.22 ), тогда

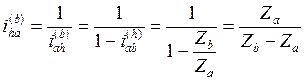
( 5.31 )

Диапазон передаточных отношений. Из формулы ( 5.31 ) имеем:

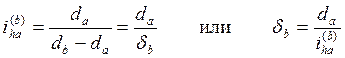
( 5.32 )

где d_B – деформация гибкого колеса.