Уравнение замкнутого векторного контура для обеих сборок:
- - - -
l1 + l2 + l3* + l4 = 0 .
Проецируя его на оси неподвижной системы координат OXY и учитывая, что j4 = 180o = Const, а xA = 1l cos j1, yA = 1l sin j1 – координаты входного шарнира A в OXY, получим:
![]() xA + l2 cos j2 + l3* cos j3 – l4 = 0 ;
xA + l2 cos j2 + l3* cos j3 – l4 = 0 ;
yA + l2 sin j2 + l3* sin j3 = 0.
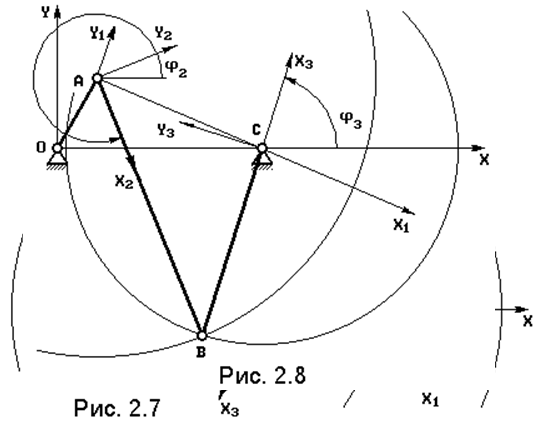
Для получения явного решения этой системы рассмотрим схемы на рис. 2.7, 2.8. В системе координат AXY запишем уравнения окружностей: первая радиусом АВ с центром в шарнире А, вторая радиусом СВ, с центром в шарнире С:
 |
![]() x2 + y2 = AB2,
x2 + y2 = AB2,
(x2 – AC) 2 + y2 = BC2,
Отсюда получаем координаты шарнира В в системе AX1Y1:
![]()
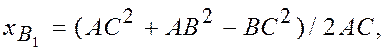
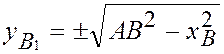 ,
,
где 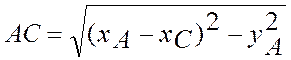 ,
,
Знак “+” соответствует прямой сборке, “–” – обратной.
Найденные xB1, yB1 преобразуем в систему OXY, как это описано в подразделе 2.4. В результате получим координаты шарнира B xB, yB. Угол для такого преобразования:
![]()
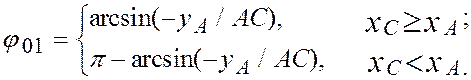
Тогда искомые углы поворота шатуна АВ и коромысла ВС:
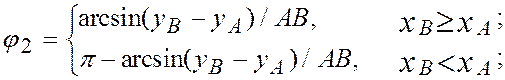
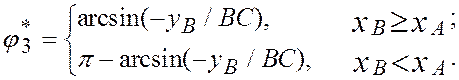
При наличии смещения CD (на рис. 2.6 показано положительное смещение) угол поворота коромысла BC :
j3 = j3* + ¡ ; ( 2.14 )
где ¡ = arctg(CD / l3 ).
Для определения угловых скоростей шатуна AB и коромысла BC продифференцируем систему ( 2.9 ) по времени :
![]() VAx –
l2 w2 sin j2 – l3* w3 sin j3 = 0 ;
VAx –
l2 w2 sin j2 – l3* w3 sin j3 = 0 ;
VAy + l2 w2 cos j2 + l3* w3 cos j3 = 0.
где: VAx= – l1 w1 sin j1, VAy= l1 w1 cos j1 – проекции скорости входного шарнира A на оси неподвижной системы координат OXY .
Система (2.15) линейна относительно w2, w3, и легко разрешима, например, по формулам Крамера.
Дифференцируя ( 2.15 ) по времени, получим систему уравнений для определения угловых ускорений шатуна и коромысла :
![]()
![]()
![]()
![]()
![]()
где:
![]() ,
, ![]() – проекции ускорения входного шарнира А на оси
системы OXY.
– проекции ускорения входного шарнира А на оси
системы OXY.
Система ( 2.17 ) также линейна относительно неизвестных e2, e3 .
2.3.2. Структурная группа "шатун - ползун"
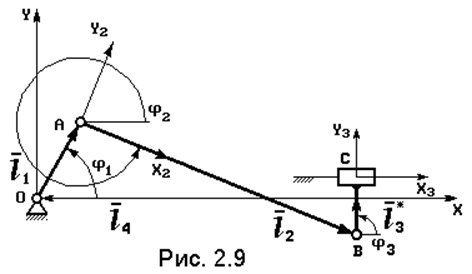 |
- - - -
l1 + l2 + l3 + l4 = 0 .
Проецируя его на оси неподвижной системы координат OXY, получим:
![]() l1
cos j1 + l2 cos j2 + l3 cos j3
+ l4 cos j4 = 0 ;
l1
cos j1 + l2 cos j2 + l3 cos j3
+ l4 cos j4 = 0 ;
l1 sin j1 + l2 sin j2 + l3 sin j3 + l4 sin j4 = 0.
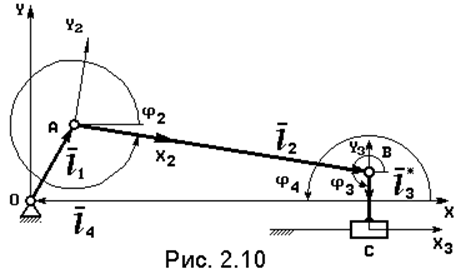 |
Угол j4= 180O = Const. Угол j3 также не меняется, но зависит от направления смещения точки B: j3 = 90О на рис. 2.9, j3 = 270O на рис. 2.10. Обозначим:
l3* = l3 sin j3 , учитывая, что
l1cos j1 = xA, l1sin j1 = yA – координаты входного шарнира, систему ( 2.17 ) запишем в виде:
![]() xA + l2 cos j2 – l4 = 0;
xA + l2 cos j2 – l4 = 0;
yA + l2 sin j2 + l3* = 0.
Так как при заданных кинематических параметрах движения входного звена угол j1, а, следовательно и xA, yA известны, то эта система легко решается относительно неизвестных j2, l4
![]() j2
= –arcsin[( l3* + yA )/ l2 ] ;
j2
= –arcsin[( l3* + yA )/ l2 ] ;
l4 = xA + l2 cos j2 .
Дифференцируя систему ( 2.18 ) по времени, получим:
![]() VAx –
l2 w2 sin j2 – VB =
0 ;
VAx –
l2 w2 sin j2 – VB =
0 ;
VAy + l2 w2 cos j2 = 0.
где: VAx, VAy – проекции скорости входного шарнира A на оси НСК OXY.
Тогда угловая скорость шатуна и скорость ползуна:
![]() w2 = –VAy /( l2
cos j2 ) ;
w2 = –VAy /( l2
cos j2 ) ;
VB = VAx – l2 w2 sin j2 .
Дифференцируя ( 2.20 ) по времени, получим систему уравнений для определения ускорений:
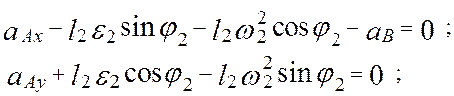
где: aAx, aAy– проекции ускорения входного шарнира A на оси НСК OXY (см. уравнение (2.16) .
Тогда угловое ускорение шатуна и ускорение ползуна:
![]()
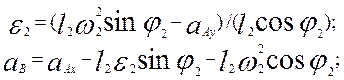
2.3.3. Кулисные структурные группы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.