Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 38

В дальнейшем будут использоваться результаты резонансных испытаний. Из теории колебаний известно (см., например [ 10, 12 ]), что при резонансе амплитуда колебаний такой системы:

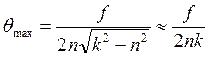
( 6.14 )

Приближенное равенство в выражении ( 6.14 ) справедливо для так называемых слабо демпфированных систем, когда k >> n. Балансировочные станки конструктивно выполняются именно такими.

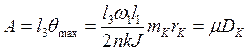В процессе экспериментов датчиком 6 (см. рис. 6.5) будет замеряться не угол поворота рамы, а амплитуда колебаний точки установки датчика:

( 6.15 )

Таким образом, мы показали, что амплитуда A резонансных колебаний пропорциональна дисбалансу D_K с некоторым пока неизвестным коэффициентом пропорциональности m.

Для нахождения величины дисбаланса D_K применим метод трех разгонов.

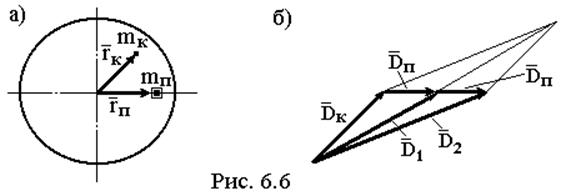
Ротор устанавливают на балансировочный станок так, чтобы плоскость I проходила через шарнирную опору 4. Двигателем 3 ротор разгоняют в зарезонансную область, т.е. до частоты вращения w₁ заведомо большей, чем k и дают выбег. В процессе выбега, когда ротор медленно тормозится система проходит через резонанс w₁ = k. Датчиком 6 замеряют амплитуду резонансных колебаний. Обозначим ее: A_K.

Далее на роторе устанавливают дополнительную, так называемую пробную массу известной величины m_П. После этой операции ротор получает дисбаланс:                                             _      _       _

D₁ = D_K + D_П                                               ( 6.16 )

Производят второй разгон ротора, дают выбег и замеряют амплитуду резонансных колебаний. Обозначим ее: A₁.

После этого на роторе в то же место устанавливают удвоенную пробную массу 2m_П. После этой операции дисбаланс ротора:

_      _       _

D₂ = D₁ + D_П                                               ( 6.17 )

Производят третий разгон ротора, дают выбег и замеряют амплитуду резонансных колебаний. Обозначим ее: A₂.

Изобразим ситуацию графически. На рис. 6.6а представлен ротор и показан изначальный дисбаланс, характеризующийся неизвестными параметрами m_K, r_K и пробные массы m_П, 2m_П, расположенные на известном расстоянии r_П.

На рис. 6.6б изображен план дисбалансов в соответствии с выражениями ( 6.16 ), ( 6.17 ). Тонкими линиями план дисбалансов достроен до параллелограмма. По свойству сторон и диагоналей параллелограмма имеем:

D_K² + D₂² = 2 D_П² + 2 D₁²

Отсюда

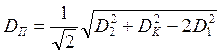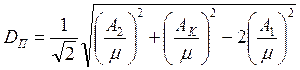или

Отсюда

                               

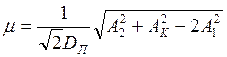
                                    ( 6.18 )

Таким образом, при известном дисбалансе пробной массы D_П и полученных в результате экспериментов значений амплитуд резонансных колебаний A_K, A₁, A₂ по формуле ( 6.18 ) находим коэффициент m. Тогда из выражения (6.15) определяем дисбаланс ротора:

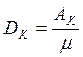Для уравновешивания надо в плоскости II установить противовес, имеющий дисбаланс такой же по величине, но противоположный по направлению.

После этого, ротор переустанавливается так, что меняются местами плоскости I – II и все описанные операции повторяются для расчета и установки противовеса в плоскости I.

Глава  7

Динамика машин с абсолютно жесткими звеньями

Динамика как раздел механики изучает движение тел под действием сил во времени. Это очень обширный раздел, в котором рассматривается много различных задач. Здесь мы рассмотрим только одну из них.

7.1. Постановка  задачи

Рассмотрим машинный агрегат, представленный на рис. 7.1, состоящий из двигателя, передаточного зубчатого механизма и исполнительного рычажного механизма. Пусть эта машина совершает установившееся движение, характеризующееся периодическими изменениями кинематических параметров движения. При этом период изменения равен рабочему циклу машины, т.е. промежутку времени, через который повторяются все фазы ее технологического процесса, соответствующему, например, времени оборота кривошипа главного рычажного механизма.

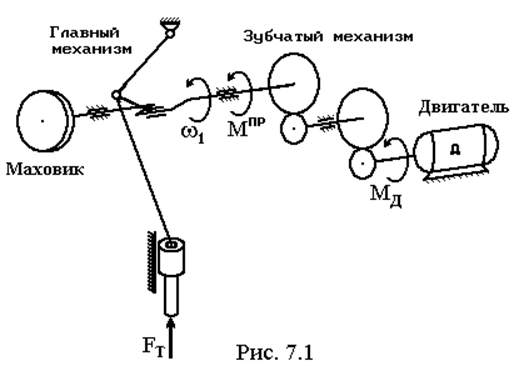Поскольку  в данном случае число степеней свободы системы W = 1, то  достаточно  определить закон движения одного ведущего  звена. Характер же движения остальных звеньев можно будет определить методами кинематики.