Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 18

Формула ( 4.8 ) показывает, что угол давления зависит и от радиуса базовой окружности кулачка R_O и от эксцентриситета e, т.е. от основных геометрических параметров. Для этого случая уже не построить такой простой алгоритм, как для механизма центрального типа.

4.7. Определение  основных  геометрических  параметров

4.7.1. Механизмы  с  толкателем  и  роликом

или с заостренным толкателем

Как уже отмечалось для механизмов этого типа (см. рис. 4.1,б,в,з) основными геометрическими параметрами являются: R_О – радиус базовой окружности кулачка и “е” – эксцентриситет. Эти величины определяют из условия ограничения угла давления [ 1, 5, 8, 9, 14, 18 ]. Для любого положения механизма текущий угол давления g, не должен превышать максимально допускаемого значения [g]. Для механизмов рассматриваемого типа обычно [g] £ 30 ... 32^o. Превышение этих значений приводит к заклиниванию механизма. При силовом замыкании механизма достаточно ограничить угол давления лишь для фазы удаления, т.к. на фазе возврата толкатель  движется  под  действием  замыкающей  силы.

На рис. 4.10 показаны диаграммы, с помощью которых можно найти величины R_О и е, такие, что всегда будет выполнено условие не заклинивания g £ [g]  [ 1, 14, 18 ] (рис. 4.10,a – для механизмов с силовым замыканием, рис. 4.10,б – с геометрическим). Здесь строится график функции S’(S), по вертикальной оси откладывается перемещение S толкателя, а по горизонтальной – производная S’ = dS/dj, называемая аналогом скорости или передаточной функцией механизма (j – угол поворота кулачка); это векторная величина, направление которой получают, повернув вектор скорости толкателя на 90° по направлению вращения кулачка. По своему физическому смыслу S’ это скорость толкателя при единичной угловой  скорости кулачка. Угол давления g_i в любом i-м положении определяется зависимостью ( 4.8 ) или в частном случае центрального механизма ( е = 0 ) – зависимостью ( 4.5 ). Схемы на рис. 4.10 фактически являются геометрической интерпретацией этих формул.

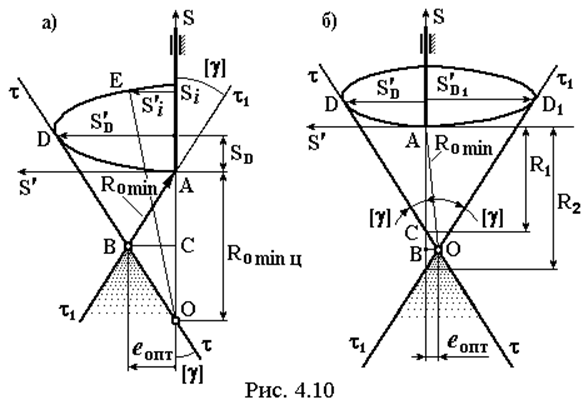Сначала рассмотрим центральный кулачковый механизм с силовым замыканием. Проведем к кривой S’(S) (см. рис. 4.10,а) касательную t-t под углом [g] к оси S. Если за положение центра вращения кулачка принять точку О пересечения прямой t-t  и оси S и считать, что центр ролика А двигается вдоль оси S, то для любого положения S_i в соответствии с формулой ( 4.5 ) текущий угол давления g_i = ÐEOS_i; по построению всегда g_i £ [g].  Поэтому минимальный радиус  базовой  окружности  R_{О min ц} центрового  профиля  при  е = 0

R_{О min ц} = çS’_Dç/tg[g] – S_D.                                            ( 4.9 )

Не увеличивая допускаемого значения угла давления, можно уменьшить размеры кулачка, вводя эксцентриситет. Наименьшее значение величины R_o будет в том случае, когда в крайнем нижнем положении центра ролика (точка А на рис. 4.10) угол давления равен [g]. Тогда минимальный радиус базовой окружности и оптимальное значение эксцентриситета определятся из треугольника  OBC:

R_{О min} = R_{О min ц} / (2cos[g] );    е_опт = R_{О min} / sin[g].                   ( 4.10 )

Линии t-t и t₁-t₁ ограничивают зону, в которой может располагаться  центр  вращения  кулачка  (на рис. 4.10 эта зона оттенена).

При геометрическом замыкании механизма условие ограничения угла давления должно выполняться как для фазы удаления, так и для фазы возврата. Определение величин R_О, е для этого случая показано на рис. 4.10,б. Касательные t-t  и  t₁-t₁ к кривой S’(S) ограничивают зону, в которой может располагаться центр вращения кулачка и отсекают от оси S отрезки R₁ и R₂, величины которых определяются по формуле ( 4.9 ). Вершина зоны определяет минимальные габариты. Оптимальное значение эксцентриситета и минимальный радиус базовой окружности получаем из треугольников  CBO  и  OAB:

( 4.11 )