Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 34

где M _ТРj, n_j – момент трения и частота вращения j-го подшипника; n_П – количество подшипников в опоре (редукторе); (Mn)_РО – произведение момента и частоты вращения рабочего органа.

Приближенное значение момента трения определяют из зависимости

M _ТР = 0,5f F_r d

где f  – коэффициент трения в подшипнике (см. [ 2 ]);

     F_r – радиальная нагрузка на подшипник;

     d – внутренний диаметр подшипника.

Потери на перемешивание и разбрызгивание масла для цилиндрических передач с внешним зацеплением, смазываемых окунанием при погружении зубчатого колеса на глубину (2…3)m, приближенно определяется по формуле [16]

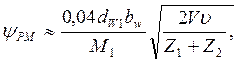
( 5.42 )

где u  – кинематическая вязкость масла при рабочей температуре, м²/с;

      М₁ – крутящий момент, Нм;

      V  – окружная скорость, м/с;

     линейные размеры берутся в мм.

При струйной смазке значения y_РМ, найденные по формуле ( 5.42 ) надо умножить на коэффициент 0,7.

Таким образом, общий коэффициент потерь для большинства зубчатых механизмов с неподвижными осями колес находят как сумму трех коэффициентов потерь:

y = y_З + y_П + y_РМ

5.10.2. КПД планетарных зубчатых механизмов

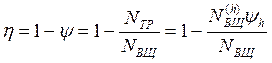КПД планетарных зубчатых механизмов выражают через коэффициент потерь механизма с остановленным водилом. Действительно

( 5.43 )

где N_ТР – мощность сил трения, N_ВЩ – мощность на ведущем колесе, N_ВЩ^(h) – мощность на ведущем колесе механизма с остановленным водилом, y_h – коэффициент потерь механизма с остановленным водилом (определяется, как это описано в п. 5.10.1).

Из выражения ( 5.43 ) можно получить формулы для КПД конкретных механизмов. Например, для механизма схемы A_ah^b (см. рис. 5.15)

N_ВЩ = M_a w_a,   N_ВЩ^(h) = M_a (w_a – w_h).

Тогда

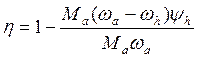
Преобразовывая это выражение, получаем

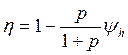
где p = –i_ab^(h) – параметр передачи.

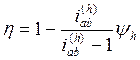
Аналогично, для других механизмов, например, для схемы B_ah^b можно получить:

5.11. Дифференциальные зубчатые механизмы

Дифференциальными называются зубчатые механизмы, в составе которых имеются колеса с подвижными осями, и имеющие число степеней свободы W = 2.

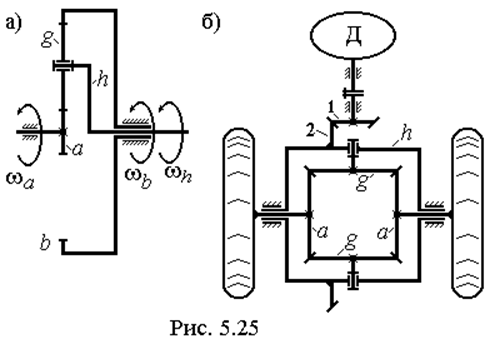
Простейшую схему дифференциального механизма (рис. 5.25а) получим из планетарного схемы A_ah^b (см. рис. 5.15а), если предоставим свободу вращения колесу b, которое в планетарном механизме неподвижно. Для определенности будем полагать, что входными звеньями являются центральные колеса a и b, а выходным – водило h.

В данном случае задача кинематического анализа формулируется в общем виде: по известным значениям параметров движения входных звеньев определить параметры движения выходного звена.

Задача по определению скоростей линейна, следовательно, выполняется принцип суперпозиции. Угловая скорость водила w_h состоит из двух компонент: одна составляющая w_h^(a) определяется вращением колеса a, а другая w_h^(b) – вращением колеса b:

w_h = w_h^(a) +  w_h^(b).

Для определения составляющих рассмотрим соответствующие планетарные механизмы A_ah^b и A_bh^a (см. рис. 5.15а,б).

w_h^(a) = w_a i_ha^(b),

w_h^(b) = w_b i_hb^(a).

Передаточные i_ha^(b), i_hb^(a) отношения определяются так, как это описано выше.

На рис. 5.25б в качестве примера, представлена схема одного из наиболее широко применяемых дифференциальных механизмов – механизма привода колес автомобиля. Здесь Д – двигатель, вращение вала которого через конические колеса 1, 2 передается водилу h. Водило вращает оси сателлитов g и через центральные колеса a это движение передается колесам автомобиля. Рассмотренная цепь представляет собой первую степень свободы, определяющую общее движение автомобиля вперед или назад. При входе автомобиля в поворот колеса, идущие по внешнему радиусу за время поворота проходят путь больший, чем колеса, идущие по внутреннему радиусу. Поэтому, они должны иметь большую угловую скорость, т.е. правое колесо должно иметь возможность свободно вращаться относительно левого. На схеме видно, что контур конических зубчатых колес a–g–a предоставляет такую возможность – это и есть вторая степень свободы.

Глава 6

 Уравновешивание  механизмов

6.1. Постановка задач

При работе механизмов центры масс звеньев могут двигаться с ускорениями. Поэтому возникают силы инерции:

( 6.1 )