В данном случае уравновешивающие силы, по своему физическому смыслу – это усилия в осях сателлитов, вращающие водило h, а водило представляет собой одно звено с кривошипом.
Рассмотрим случай, когда вес кривошипа G1 пренебрежимо мал по
сравнению с 
.
Уравновешивающую силу найдем из условия равновесия кривошипа в виде равенства нулю суммы моментов относительно точки O:
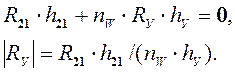
Тогда уравнение равновесия кривошипа:
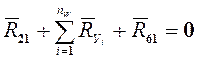(3.13)
Уравнение (3.13) решим графически, путем построения
плана сил (рис. 3.9,б). Векторы и 
откладываем в масштабе с учетом
направления. В данном случае уравновешивающие силы образуют замкнутый контур и
не влияют на величину реакции в опоре, что можно отметить как одно из
преимуществ планетарных механизмов по сравнению с рядными. Замыкая план,
находим искомый вектор 
. В данном случае, когда мы учли
только и ,
реакция в опоре кривошипа оказалась равной 
.
4.1. Классификация механизмов
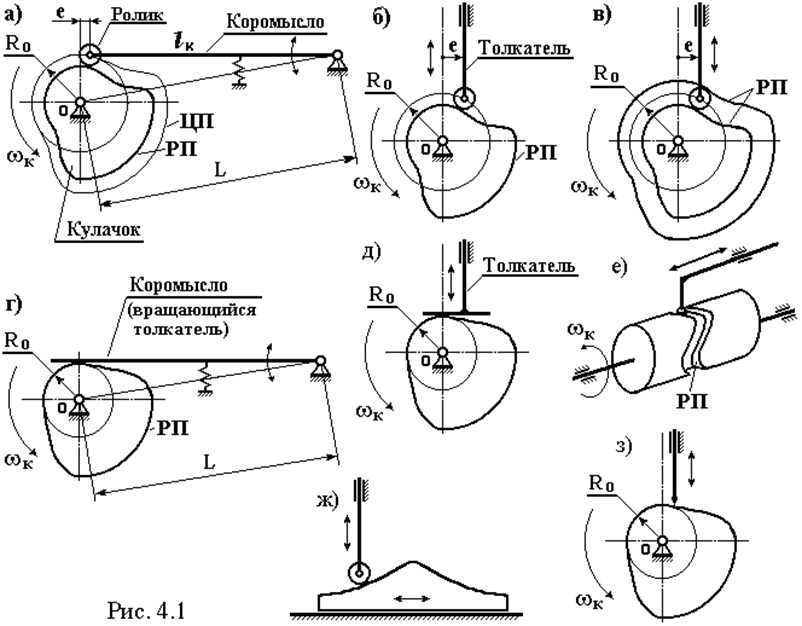
Кулачковым называется механизм, в составе которого есть асимметричное звено, называемое кулачком, рабочий профиль которого определяет кинематические свойства механизма. Примеры представлены на рис. 4.1. Звено, контактирующее с кулачком непосредственно или через ролик, называется толкателем или, если оно совершает качательные движения – коромыслом (вращающимся толкателем). Средства, применяемые для обеспечения непрерывности контакта кулачка и толкателя, называются замыканием механизма.
 |
1. По назначению.
а) Позиционные. У них в процессе работы выходное звено должно занять ряд конкретных положений (позиций). В самом простом случае они предназначенные для “переброски” выходного звена из одного крайнего положения в другое и обратно. Примером такого механизма является кулачковый механизм бензинового двигателя, открывающий и закрывающий клапан впрыска топлива.
б) Функциональные. Эти механизмы в процессе работы должны реализовывать требуемую функцию перемещения выходного звена.
2. По характеру движения кулачка:
а) Механизмы с вращающимся кулачком (рис. 4.1а-е,з).
б) Механизмы с поступательно движущимся кулачком (рис. 4.1ж). Такие кулачки часто называют копирами.
3. По характеру движения толкателя:
а) Механизмы с вращающимся толкателем (коромыслом) (рис. 4.1а,г).
б) Механизмы с прямолинейно движущимся толкателем (рис. 4.1б,в,д,е,ж,з).
4. По характеру контакта между кулачком и толкателем:
а) Механизмы с роликовым контактом (рис. 4.1а,б,в,ж).
б) Механизмы с плоским толкателем (рис. 4.1г,д).
в) Механизмы с заостренным толкателем (рис. 4.1з).
5. По типу замыкания:
а) Механизмы с силовым замыканием (рис. 4.1а,б,г,д,ж,з), когда непрерывность контакта кулачка и толкателя обеспечивается некоторой силой, например, силой прижимной пружины (рис. 4.1а,г).
б) Механизмы с геометрическим замыканием (рис. 4.1в,е), когда непрерывность контакта кулачка и толкателя обеспечивается за счет того, что толкатель или ролик толкателя движется внутри паза в кулачке.
6. По типу ведущего звена:
а) Механизмы с ведущим кулачком.
б) Механизмы с ведущим толкателем.
7. По расположению звеньев:
а) Плоские механизмы (рис. 4.1а,б,г,д,ж,з).
б) Пространственные механизмы (рис. 4.1е).
Если толкатель и кулачок контактируют через ролик, то различают следующие профили кулачка. Центровой профиль (ЦП) – траектория центра ролика на вращающейся плоскости кулачка. Рабочий профиль (РП) – профиль, по которому кулачок изготавливается.
С точки зрения структуры механизмов ролик (если он есть) является пассивным звеном и при вычислении числа степеней свободы его следует условно удалить и тогда для всех плоских механизмов, представленных на рис. 4.1 число степеней свободы по формуле Чебышева
W = 3n – 2p5 – p4 = 3 . 2 – 2 . 2 – 1 = 1
В дальнейшем мы ограничимся рассмотрением только плоских механизмов с вращающимся кулачком.
4.2. Основные геометрические параметры кулачковых механизмов
Механизмы с толкателем. У этих механизмов основными геометрическими параметрами являются:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.