Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 20

где:  S_D, S”_D – значения перемещения толкателя и аналога его ускорения, соответствующие  точке D,  в  которой  t-t  касается  S”(S).

На  практике  R_o  вбирают  несколько  большим,  чем  R_{o min} .

4.7.3. Механизмы  с  коромыслом  и  роликом

Схема такого механизма представлена на рис. 4.1а. Для этих механизмов основными  геометрическими  параметрами являются: или пара (R_O, L) или пара (R_O, l_к), где R_O – радиус базовой окружности кулачка, L – межцентровое расстояние (между центром вращения кулачка и центром качания коромысла), l_к – длина  коромысла. Также, как для механизмов с толкателем и роликом или с заостренным толкателем здесь основные геометрические параметры определяют из условия ограничения угла давления g [ 1, 14, 18 ]. Для механизмов рассматриваемого типа его предельно допускаемая величина обычно [g]  £  45 … 50^o. Превышение этих значений  приводит  к  заклиниванию  механизма.

Сначала так же, как для механизмов с толкателем, найдем связь между углом давления и основными геометрическими параметрами.

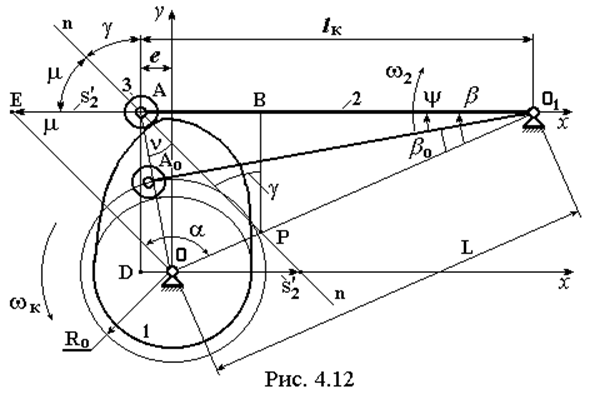На рис. 4.12 представлена расчетная схема. Найдем полюс зацепления P на пересечении нормали к профилю кулачка n-n, и линии центров ОО₁.

По оси коромысла О₁A в масштабе чертежа отложим величину аналога скорости точки A:

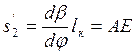                                                        ( 4.15 )

где b = b_О + y – угол поворота коромысла, отсчитываемый от линии центров ОО₁,

y – угол поворота коромысла, отсчитываемый от положения, соответствующего фазе ближнего выстоя,

j – угол поворота кулачка.

Проведем под углом передачи m луч до пересечения с линией центров. По определению углов давления и передачи в точке пересечения должна находиться ось вращения кулачка. Из построенного таким образом DОО₁E со сторонами

ОО₁ = L

О₁E = l_к + s₂’ = l_к (1 + b’)

по теореме синусов найдем:

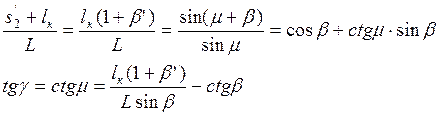
( 4.16 )

Заметим, что угол давления g зависит от соотношения l_к /L, от b и b’. При заданном законе движения коромысла величины b и b’ для каждого положения известны. Кроме того, отметим, что если центр вращения кулачка на рис. 4.12 сместить в любую точку ниже прямой OE, то угол передачи увеличится, а угол давления соответственно уменьшится.

В выражениях ( 4.16 ) в явном виде нет такого параметра как радиус базовой окружности кулачка R_О. Но в неявном виде он там присутствует, т.к. угол b зависит от угла b_О, а тот в свою очередь связан с R_О соотношением, определяемым из DОО₁A_О по теореме косинусов:

R_О² = l_к² + L² – 2 l_к L cosb_О                                ( 4.17 )

Таким образом, выражения ( 4.16 ) и ( 4.17 ) дают связь угла давления с основными геометрическими параметрами рассматриваемого механизма. В отличие от случая механизма с толкателем, рассмотренного в подразделе 4.6 здесь не удается получить столь явную и удобную форму этой связи, но полученные результаты позволят построить методику определения параметров механизма, обеспечивающих его незаклинивание.

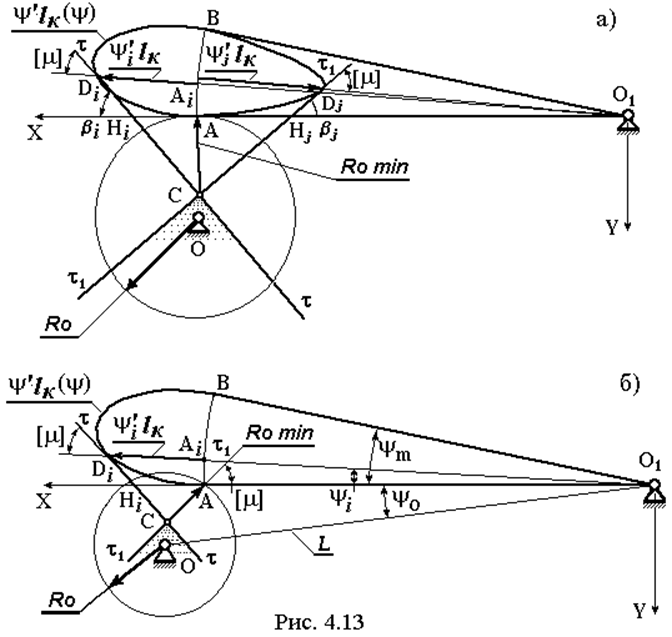На рис. 4.13 показаны расчетные схемы, с помощью которых можно найти величины R_O и L, такие, что всегда будет выполнено условие не заклинивания g £ [g]  [ 14, 18  ] (рис. 4.13a – для механизмов с геометрическим замыканием,  рис. 4.13б – с  силовым).

Угловое перемещение коромысла как функцию угла поворота кулачка y(j) и функцию y’(j) = dy/dj – аналога угловой скорости коромысла получают так, как это описано в п. 4.2. Величина s₂’ = y’l_к – аналог скорости точки А – конца коромысла – вектор, направление которого определяют, повернув вектор скорости точки А на 90° по направлению вращения кулачка, т.е. линия действия вектора y’l_к  совпадает с коромыслом ОА. Откладывая векторы y’l_к  от дуги AB – влево для фазы удаления, вправо – для фазы возврата и проведя через концы векторов плавную кривую, получим диаграмму y’l_к (y).