Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 30

Механизм схемы “А”. Различные варианты этого механизма показаны на рис. 5.15. На структурных схемах планетарных механизмов на виде сбоку (рис. 5.15а,б,в) условно принято показывать только один сателлит, хотя на самом деле их как правило не меньше трех, как это показано на рис. 5.15г; лишь в приборостроении при небольших нагрузках применяют механизмы с двумя сателлитами.

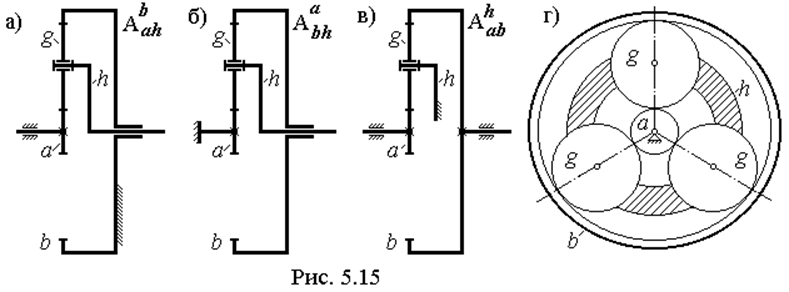
В обозначении схемы механизма применяют три индекса: нижние индексы указывают входное и выходное звено, а верхний индекс указывает – какое звено неподвижно. Примеры показаны на рис. 5.15а,б,в. Также индексируется и передаточное отношение: i_ah^(b), i_bh^(a), i_ab^(h).

У планетарного механизма сателлиты совершают сложное движение, состоящее из вращения вокруг своих осей и переносного – вращения осей сателлитов вместе с водилом. Поэтому непосредственное определение передаточного отношения, так, как это было сделано, например, для рядных механизмов, в данном случае невозможно. Для решения этой задачи применяют метод инверсии (обращенного движения), суть которого состоит в следующем. Всему механизму условно придают “минус угловую скорость водила”. В результате водило как бы останавливается и мы получаем механизм с неподвижными осями колес. Его называют механизмом с остановленным водилом (см. рис. 5.15в). Передаточное отношение этого механизма легко определяется. После чего, устанавливают связь между передаточным отношением механизма с остановленным водилом и передаточным отношением интересующего нас планетарного механизма.

Проделаем эти операции применительно к механизму схемы “A_ah^b” (см. рис. 5.15а). После остановки водила получаем механизм “A_ab^h”, показанный на рис. 5.15в. Это механизм с промежуточным колесом, одним внешним и одним внутренним зацеплением, его передаточное отношение:

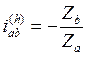Попутно отметим, что передаточное отношение механизма с остановленным водилом взятое с обратным знаком, называют параметром планетарной передачи:    p = –i_ab^(h).

Для установления связи между передаточными отношениями механизмов A_ah^b и A_ab^h обозначим: w_a – угловая скорость колеса a в в механизме A_ah^b, w_a*– угловая скорость колеса a в в механизме A_ab^h, и рассмотрим передаточное отношение последнего “по определению”:

Таким образом, мы получили основную формулу для определения передаточных отношений планетарных механизмов класса 2k-h.

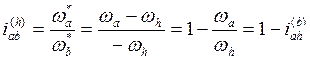( 5.22 )

Тогда для механизма A_ah^b имеем:

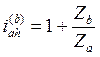
( 5.23 )

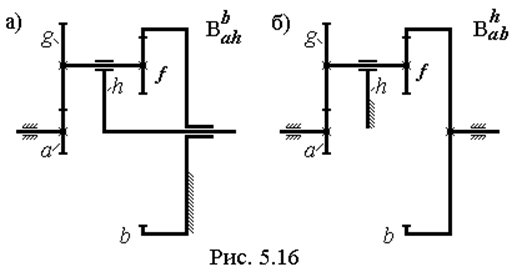
Механизм схемы “B”. Структурная схема этого механизма показана на рис. 5.16а. Проделаем еще раз, применительно к этому механизму операции по методу инверсии.

После остановки водила получаем механизм B_ab^h, показанный на рис. 5.16б. Это рядный механизм с одним внешним и одним внутренним зацеплением, его передаточное отношение:

Тогда по формуле ( 5.22 ) для механизма схемы B_ah^b, получаем:

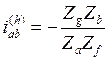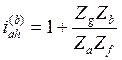
( 5.24 )

Механизм схемы “С”. Структурная схема этого механизма показана на рис. 5.17а.

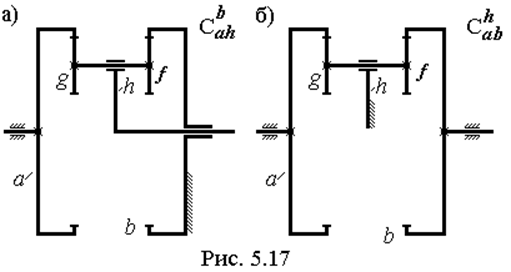После остановки водила получаем механизм С_ab^h, показанный на рис. 5.17б. Это рядный механизм с двумя внутренними зацеплениями, его передаточное отношение:

Тогда по формуле ( 5.22 ) для механизма схемы С_ah^b, получаем:

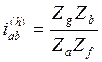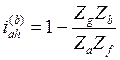
Однако механизм схемы “C” работоспособен только в направлении от водила к колесу a, передаточное отношение в этом случае

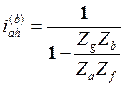
( 5.25 )

При проектировании планетарных зубчатых механизмов, в частности при подборе чисел зубьев, необходимо выполнять некоторые дополнительные условия.

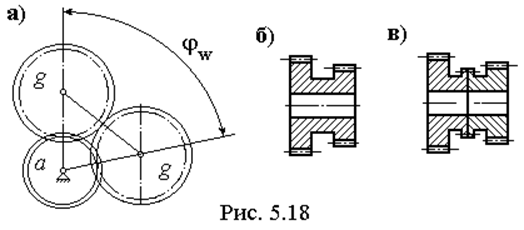
Условие соосности. Входной и выходной валы механизма должны иметь одну геометрическую ось. Для схемы A это условие выражается как:

Z_a + Z_g = Z_b – Z_g

Для схемы B:                    m_ag(Z_a + Z_g) = m_fb(Z_b – Z_f )                                    ( 5.26 )

Для схемы C:                    m_ag(Z_a – Z_g) = m_fb(Z_b – Z_f)

Условие соседства сателлитов. Это условие должно проверяться только при числе сателлитов n_W > 3, т.к. при n_W £ 3 оно выполняется автоматически. Его физический смысл состоит в том, что между окружностями выступов двух соседних сателлитов должен быть зазор.