Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 29

p_{n =} p_t / cos b_W

На рис. 5.12б построен план скоростей для контактной точки, совпадающей с полюсом зацепления “p”.

Из D pV_nV₁:   V_n = V₁ cos b_W1

из D pV_nV₂:    V_n = V₂ cos b_W2

Следовательно:     V₁ cos b_W1 = V₂ cos b_W2

или                      w₁R₁ cos b_W1 = w₂ R₂ cos b_W2

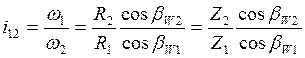Тогда передаточное отношение:

( 5.18 )

Отметим, что для данного механизма передаточное отношение зависит не от 2-х, а от 4-х параметров.

Червячная передача

Эта передача применяется для передачи вращения между валами с перекрещивающимися валами, когда угол скрещивания S = 90^O (рис. 5.13). Червячная передача – это частный случай винтовой. Здесь угол наклона зубьев 1-го колеса весьма велик: b_W1 = 80^O … 88^O. При этом винтовая линия зуба 1-го колеса несколько раз опоясывает делительный цилиндр. Такое колесо называют червяком, а такие зубья называют витками или нитками. Каждый виток имеет начало на торце колеса, и его называют заходом (a₁). Количество заходов червяка является аналогом количества зубьев на колесе.

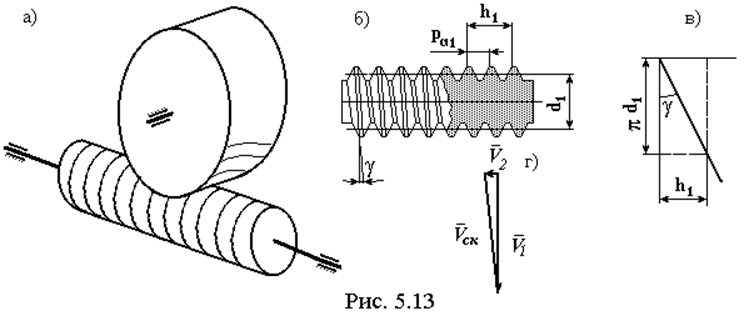Сопряженное с червяком колесо называется червячным колесом. Т.к. S = b_W1 + b_W2 = 90^O, то угол b_W2  мал и червячное колесо приближается к цилиндрическому. Для червяка угол подъема винтовой линии g = b_W2.

Геометрические соотношения в червяке

Количество заходов: a₁ = 1 … 4;

d₁  - диаметр начального цилиндра;

p_a – осевой шаг червяка: расстояние двумя одноименными точками двух соседних профилей, измеренное вдоль оси червяка;

h₁ = a₁ p_a – ход червяка: расстояние двумя одноименными точками соседних профилей витка.

Развернем виток червяка на плоскость в пределах одного поворота (рис. 5в).

где q – коэффициент диаметра червяка.

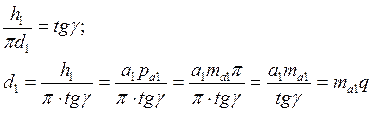Передаточное отношение:

_      _       _       _       _

V₂ = V₁ + V₂₁ = V₁ + V_СК

На рис. 5г представлен план скоростей, соответствующий этому векторному уравнению.

Тогда

Диапазон передаточных отношений червячной передачи весьма широкi₁₂ = 20 …200, но КПД, вследствие большого скольжения, довольно низок.

5.8. Кинематический анализ зубчатых механизмов

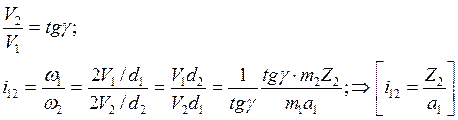Применительно к зубчатым механизмам кинематический анализ сводится к определению их передаточных отношений.

5.8.1. Рядные  механизмы

Пример механизма типа простой зубчатый ряд представлен на рис 5.14,а. Определим его передаточное отношение, применив искусственное преобразование.

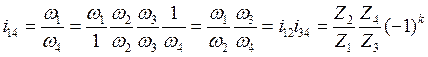
( 5.19 )

где k – количество внешних зацеплений.

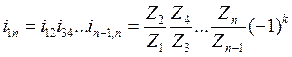Обобщая формулу ( 5.19 ) на произвольное число ступеней “n”, получим:

( 5.20 )

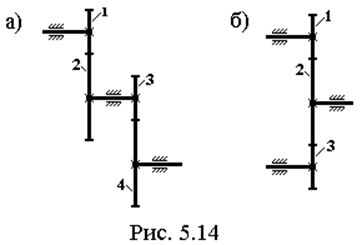
Таким образом, передаточное отношение механизма типа простой зубчатый ряд равно произведению передаточных отношений ступеней.

Этот вывод можно еще более обобщить: при последовательном соединении механизмов общее передаточное отношение равно произведению передаточных отношений соединяемых механизмов.

5.8.2. Механизмы с промежуточными колесами

Пример такого механизма представлен на рис 5.14б, где колесо 2 – промежуточное. Определим его передаточное отношение, применив аналогичное искусственное преобразование.

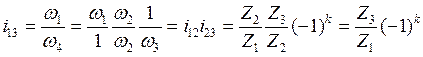
( 5.21 )

Таким образом, передаточное отношение механизма с промежуточными колесами не зависит от параметров промежуточных.

5.8.3. Планетарные зубчатые механизмы

Планетарными называются механизмы, в составе которых есть колеса с подвижными осями. Приведем основные термины.

Колеса, оси которых неподвижны, называются центральными. Одно из центральных колес в планетарных механизмах – неподвижно. Колеса, оси которых подвижны, называются сателлитами. Звено, в котором устанавливаются оси сателлитов, называется водилом. Для схем планетарных механизмов приняты стандартизованные обозначения. Центральные колеса индексируются буквами a, b, e, сателлиты – g, f, водило индексируется буквой h.

Существуют различные классы планетарных механизмов. Эти классы имеют общие обозначения, в которых указывается – какие звенья являются основными, т.е. участвующими в передаче крутящего момента. Например, у механизмов класса 2k-h основными являются 2 центральных колеса и водило; у механизмов класса 3k – 3 центральных колеса. Здесь мы рассмотрим только наиболее простые механизмы – класса 2k-h.