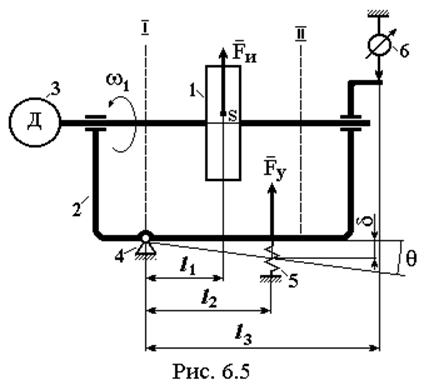
Уравновешивание роторов на балансировочных станках. Существуют различные типы балансировочных станков. Мы рассмотрим один из вариантов. На рис. 6.5 представлена схема балансировочного станка, где 1 – ротор, 2 – рама балансировочного станка, 3 – двигатель, вращающий ротор, 4 – жесткая шарнирная опора, 5 – упругая опора, 6 – датчик, замеряющий амплитуду колебаний рамы, I и II – плоскости, в которых конструкцией ротора предусмотрена возможность постановки противовесов для уравновешивания ротора. Точка S – центр масс ротора, который может быть смещен относительно оси вращения на некоторую величину. Фактически требуется каким-то образом определить величину имеющегося остаточного дисбаланса и устранить его установкой противовесов.
Принципиально последовательность действий можно представить следующим образом.
1. Создать математическую модель балансировочного станка с установленным на нем уравновешиваемым ротором как механической колебательной системы.
2. Произвести эксперименты с уравновешиваемым ротором.
3. На основании данных экспериментов с помощью математической модели определить фактический дисбаланс.
4. Установить противовесы, устраняющие имеющийся дисбаланс.
Для решения этой задачи будут проводиться тестовые испытания с исследованием резонансных колебаний рамы станка, поэтому сначала составим математическую модель балансировочного станка как механической колебательной системы.
Создание математической модели будет состоять из следующих этапов.
1. Формирование дифференциального уравнения колебаний рамы станка под действием инерционной нагрузки от неуравновешенного ротора.
2. Нахождение его решения при резонансе.
3. Определение связи между замеряемой амплитудой колебаний, найденным решением и дисбалансом.
 |
Уравнение колебаний рамы составим, опираясь на Принцип д’Аламбера. Уравнение квазиравновесия по д’Аламберу:
MУ + MС + MВН = MИ ( 6.6 )
где MУ – момент, создаваемый силами упругости, MС – момент, создаваемый силами сопротивления, MВН – момент, создаваемый внешними силами, MИ – момент сил инерции.
Рассмотрим каждое слагаемое уравнения ( 6.6 ).
![]()
( 6.7 )
где J – момент инерции рамы станка вместе с установленным на нем ротором и двигателем относительно оси качания рамы, q – угол поворота рамы в процессе колебаний.
Внешней силой, вызывающей колебания рамы является сила инерцииFИ, возникающая при вращении ротора из-за наличия дисбаланса. Момент ею создаваемый:
MВН = FИl1 sin w1t = – mKaS l1 sin w1t
где mK – неуравновешенная масса (неизвестна), aS – ускорение центра масс ротора, w1 – угловая скорость вращения ротора.
Если w1 близка к постоянной, то полное ускорение состоит только из нормальной составляющей aS » aSn и
MВН » – mK aSn l1 sin w1t = – mK w12 rK l1 sin w1t ( 6.8 )
где rK – радиус расположения неуравновешенной массы (неизвестен).
В процессе колебаний деформируется упругая опора 5, которая создает силу FУ. Момент, который при этом возникает:
MУ = FУl2 = C dl2 » C l22 q ( 6.9 )
где C – коэффициент жесткости пружины, d – деформация упругой опоры.
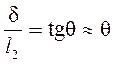 |
Для момента сил сопротивления MС примем гипотезу вязкого трения, в соответствии с которой этот момент пропорционален скорости:
![]()
( 6.10 )
где h – коэффициент демпфирования.
Подставляя выражения ( 6.7 ) … ( 6.10 ) в уравнение ( 6.6 ) получаем:
![]()
( 6.11 )
или
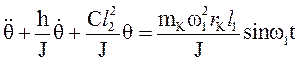
( 6.12 )
Обозначим: h / J = 2n, C l22 / J = k2, mKw12 rK l1 / J = f, тогда
![]()
( 6.13 )
где n – коэффициент затухания, k – собственная частота.
Уравнения ( 6.11 ) … ( 6.13 ) и являются искомой математической моделью процесса колебаний рамы балансировочного станка. Это линейные дифференциальные уравнения второго порядка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.