Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 21

Найдем область возможных положений точки О – центра вращения кулачка. Пусть для некоторого угла поворота кулачка j_i угол поворота коромысла на фазе удаления y_i. Если через точку D_i – конец вектора y’l_к  провести прямую t-t  под углом [m] = 90° – [g] к вектору O_iD_i  (см. рис. 4.8), то для данного угла j_i  t-t – геометрическое место предельно возможных положений точки O; если центр вращения кулачка будет располагаться на этой прямой, то в данном положении g = [g], если левее – g < [g],  правее – g > [g]. Аналогично, для любого j-го положения на фазе возврата для механизма с геометрическим замыканием прямая t₁-t₁ определяет геометрическое место предельно возможных положений точки O, но в этом случае g < [g], когда центр вращения кулачка правее прямой t₁-t₁.

Для механизма с геометрическим замыканием (см. рис. 4.13а), проводя прямые t-t  и t₁-t₁ для всех рассматриваемых положений, выбирают такое их сочетание, когда величина AC будет наибольшей; такое сочетание и определит  область  возможных  положений  точки  О.

Для механизма с силовым замыканием (см. рис. 4.13б), когда угол давления ограничивается лишь на фазе удаления, положение прямой t₁-t₁ фиксировано (y_j = 0), а варьируется лишь положение t-t. Этот вариант является частным случаем предыдущего, поэтому рассмотрим вариант механизма с геометрическим  замыканием  как  более  общий.

Введем неподвижную систему координат OXY, направление оси X соответствует положению коромысла при y = 0. Если угол поворота коромысла y_i на фазе удаления и уголy_j на фазе возврата соответствуют предельным положениям прямых t-t  и t₁-t₁  (см. рис. 4.13а), то искомые величины R_O, L определяются после вычисления координат  x_C, y_C  точки C, которые найдем совместным решением уравнений прямых t-t   и t₁-t₁.

Уравнение  прямой  t-t

y = tg b_i (O₁H_i – x),                                                 ( 4.18 )

где b_i = [m] + y_i.

Выражая  величину  O₁H_i  через  известные  параметры,  получим

y = l_к (1+ y’_i)( tg b_i cos y_i – sin y_i) – x tg b_i.                            ( 4.19 )

Аналогично,  для  прямой  t₁-t₁

                y = tg b_j (x – O₁H_j );

y = x tg b_j – l_к (1+y’_j)( tg b_j cos y_j + sin y_j).                            ( 4.20 )

где b_j = [m] – y_j.

Приравнивая правые части уравнений ( 4.19 ) и ( 4.20 ), найдем координату  x_C  точки  О:

x_C = l_к [(1+y’_i)(tg b_i cos y_i – sin y_i) + (1+y’_j)(tg b_j cos y_j + sin y_j)]/(tg b_i + tg b_j)

( 4.21 )

тогда координата y_C – значение правой части выражения ( 4.19 ) при x = x_C .

Точка  А  имеет  координаты  А(l_к,0),  следовательно,

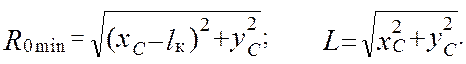                       ( 4.22 )

При проектировании кулачковых механизмов возможны ситуации, когда межцентровое расстояние L заранее выбрано из конструктивных соображений. В этом случае необходимо найти такой радиус R_O, который позволил бы сохранить выбранное значение L. Очевидно, что решение будет получено, если найти координаты точек пересечения окружности радиуса L с центром в точке О₁ с прямой t-t (L < O₁C) или с t₁-t₁ (L > O₁C); при этом из двух точек пересечения прямой с окружностью следует выбирать точку с большим значением x. Если прямая и окружность заданы уравнениями y = ax + b;  x² + y² = L²,  то абсциссы x_п1,2 точек их пересечения

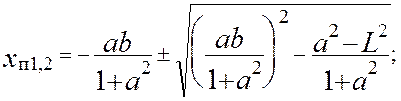                               ( 4.23 )

из двух значений x_п выбираем большее, тогда y_п = ax_п + b. Величины a и b вычисляются  в  соответствии  с  выражениями ( 4.19 ), ( 4.20 ):

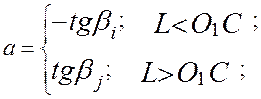
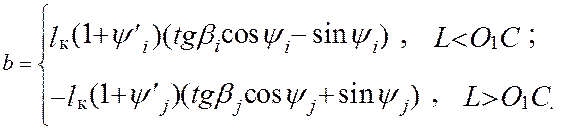
Радиус  базовой  окружности  в  этом  случае

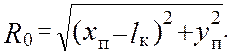                                                 ( 4.25 )

На практике обычно центр вращения кулачка точку О располагают внутри допустимой зоны (см. рис. 4.13), обеспечивая тем самым некоторый запас по углу давления. Если межцентровое расстояние L заранее не задано, то точку О целесообразно располагать на равном удалении от прямых t-t, t₁-t₁. Расчет ее положения аналогичен описанному выше расчету положения точки С, надо лишь параллельно сместить прямые t-t , t₁-t₁ внутрь зоны. Обозначим:  K_C  ³ 1 – коэффициент запаса.  Тогда  формулы ( 4.19 ) . . . ( 4.22 ) примут  вид [ 5 ]: