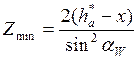 |
Формула ( 5.12 ) показывает, что введение положительного смещения позволяет уменьшить минимальное число зубьев. Однако, при увеличении положительного смещения возможно возникновение другого недопустимого явления – заострения зуба (рис. 5.7д). Зуб является заостренным, если полка на вершине зуба составляет меньше, чем (0,2…0,4)m.
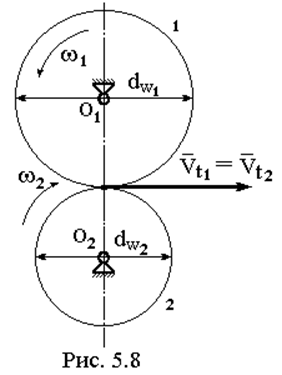 При выводе формул для определения передаточных отношений будем
опираться на его определение.
При выводе формул для определения передаточных отношений будем
опираться на его определение.
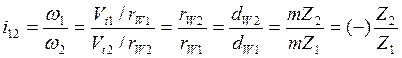 |
где m – модуль, Z1, Z2 – числа зубьев колес.
Этому передаточному отношению приписывается знак “–” для внешнего зацепления, т.к. при этом изменяется направление вращения и знак “+” для внутреннего зацепления, т.к. при этом направление вращения не изменяется.
5.7.2. Пространственные зубчатые передачи
Пространственными называются зубчатые механизмы, позволяющие передавать вращение между валами, расположенными в различных плоскостях. К ним относятся:
1. Конические зубчатые передачи.
2. Винтовые.
3. Червячные.
И некоторые другие.
5.7.2.1. Конические зубчатые передачи
 |
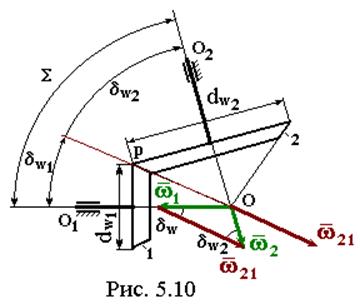 |
Связь между векторами угловых скоростей w1 и w2 звеньев 1 и 2:
_ _ _
w2 = w1 + w21 ( 5.14 )
гдеw21 - угловая скорость звена 2 относительно звена 1.
На рис. 5.10 представлен план угловых скоростей, соответствующий векторному уравнению ( 5.14 ). Положение вектора w21 относительно векторов w1 и w2 определяется углами dW1, dW2, сумма которых равна межосевому углу S:
dW1 + dW2 = S ( 5.15 )
Если вектор w21 перенести в точку O пересечения осей колес, то он совпадет с мгновенной осью OP относительного движения звеньев и определит конические поверхности, называемые начальными конусами.
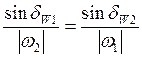 |
Поскольку отношение угловых скоростей по определению называется передаточным отношением, то
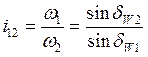
( 5.16 )
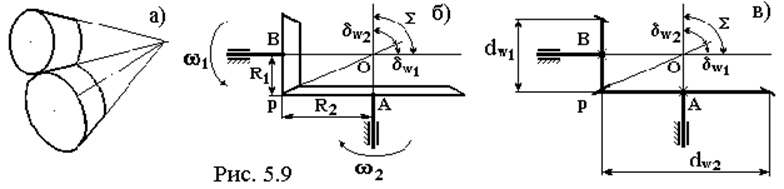
Для ортогональной передачи (см. рис. 5.9,б) из DOPA: R2 = OP sin dW2
из DOPB: R1 = OP sin dW1
Тогда
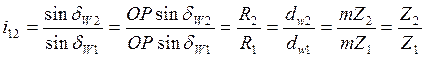
( 5.17 )
Основные параметры
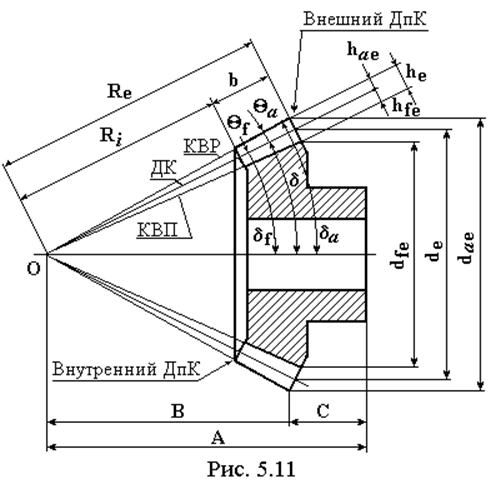
Схема конического зубчатого колеса представлена на рис. 5.11, где приняты следующие обозначения.
ДК – делительный конус,
КВР – конус вершин,
КВП – конус впадин,
Внешний и внутренний ДпК – внешний и внутренний дополнительные конусы.
Все параметры колеса измеряются по внешнему ДпК, что отмечается индексом “e” в обозначениях параметров.
5.7.2.2. Гиперболоидные зубчатые передачи
Геометрическое место положений мгновенных осей вращения называют аксоидом. В зубчатой передаче со скрещивающимися осями колес при постоянном передаточном отношении аксоидами относительного движения являются однополюсные гиперболоиды вращения. Поэтому зубчатые передачи со скрещивающимися осями колес называют гиперболоидными.
Винтовая передача
Эта передача состоит из двух эвольвентных цилиндрических косозубых колес (рис. 5.12), оси которых скрещиваются в общем случае под произвольным углом S. Межосевой угол
S = bW1 ± bW2
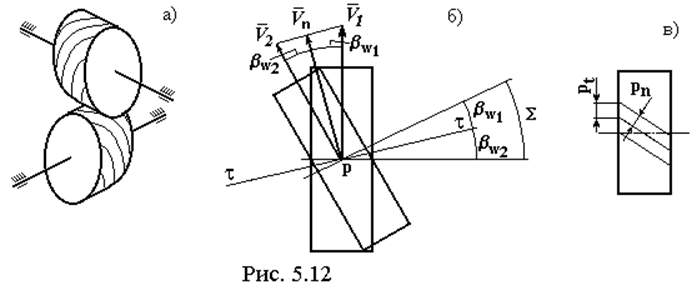 |
В частном случае ортогональной передачи S = bW1 ± bW2 = 90O.
Как для любых косозубых колес в данном случае различают торцевой pt и нормальный pn шаг зацепления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.