Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 45

d_ПР = d₁ + d₂                                              (  8.6 )

Общий коэффициент жесткости (рис. 8.6г):

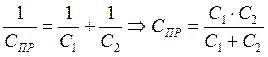8.4. Линейные  и  нелинейные  жесткостные  характеристики

Выше, когда мы вводили понятие коэффициента жесткости, то полагали, что это константа. Однако, это далеко не всегда так. Более того, коэффициент жесткости в точности постоянен только тогда, когда упругий элемент изготовлен из стали и испытывает только упругие деформации в пределах закона Гука и в упругой связи нет зазоров. Во всех остальных случаях в той или иной степени имеет место нелинейность. Другое дело, что немало случаев, когда эта нелинейность не велика, и ею можно пренебречь.

Видов нелинейности характеристик упругих связей весьма много. Здесь мы рассмотрим два наиболее часто встречающихся:

1. Наличие зависимости коэффициента жесткости от степени деформации упругого элемента.

2. Зазоры.

На рис. 8.7,а,б показана линейная жесткостная и соответствующая ей силовая характеристика F_C(x), т.е. график силы, создаваемой упругим элементом при его деформировании. Такие и только такие характеристики упругих элементов называются линейными.

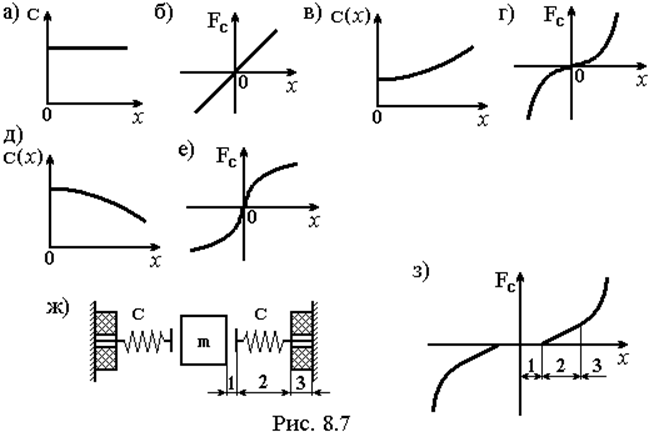
На рис. 8.7,в,г показана жесткостная и соответствующая ей силовая характеристика F_C(x), для которых характерно увеличение коэффициента жесткости при увеличении степени деформации упругого элемента. Такие характеристики принято называть жесткими. Они характерны, например, для упругих элементов из полимерных материалов, в частности для резин, работающих на сжатие.

На рис. 8.7,д,е показаны характеристики, для которых характерно уменьшение коэффициента жесткости при увеличении степени деформации упругого элемента. Такие характеристики принято называть мягкими.

Для жесткостных характеристик представленных на рис. 8.7,а,в,д можно получить приближенные аналитические описания, например, в виде полиномов вида:

C(x) = C₀ + C₁x + C₂x² + …                               ( 8.7 )

На практике могут встречаться всевозможные комбинации различных видов нелинейностей. На рис. 8.7,ж изображена масса m, амортизация которой осуществляется с помощью пружин C и амортизирующих прокладок из полимерного материала. При этом между массой и пружиной есть зазор. Вид силовой характеристики такой подвески показан на рис. 8.7,з. Она состоит из участков с различным характером зависимости F_C(x). Участок 1 – масса движется в пределах зазора, упругого сопротивления движению нет. Участок 2 – зазор выбран, работает пружина с линейной характеристикой (коэффициент жесткости постоянен). Участок 3 – масса дошла до полимерной прокладки, характеристика жесткости которой на сжатие имеет нелинейный, жесткий вид.

8.5. Способы  учета  рассеяния  энергии  при  колебаниях

Динамические модели, которые учитывают рассеяние энергии при колебаниях, называются диссипативными.

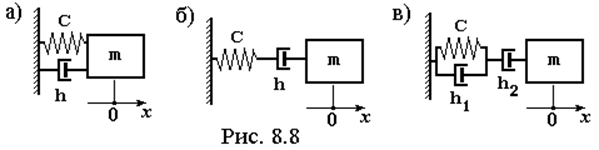
Самым простым и распространенным способом учета рассеяния энергии является введение в динамическую модель отдельного демпфирующего элемента h (рис. 8.8), где h – как уже отмечалось это коэффициент демпфирования.

Демпфирующий элемент в дискретную модель может быть введен по-разному. На рис. 8.8,а он поставлен параллельно упругому элементу – это модель Кельвина-Фойгхта. На рис. 8.8,б он поставлен последовательно с упругим элементом – это модель Максвелла. Иногда применяют и более сложные сочетания, например, такие, как показано на рис. 8.8,в. Благодаря своей простоте наиболее распространенной является модель Кельвина-Фойгхта.

Вид демпфирующей характеристики зависит от принятой гипотезы рассеяния энергии. Наиболее распространенной, опять же благодаря своей простоте является гипотеза вязкого трения, в соответствии с которой предполагают, что сила, создаваемая демпфирующим элементом пропорциональна скорости деформации:

F_h = h                                                     ( 8.8 )

где h – коэффициент пропорциональности, называемый коэффициентом демпфирования, и имеющий в данном случае размерность [H c/м].

Другой распространенной гипотезой является гипотеза сухого трения, в соответствии с которой предполагают, что сила, создаваемая демпфирующим элементом постоянна по величине, но меняет свой знак при изменении знака скорости деформации: