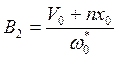Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 47

и при t = 0 получаем

Решение ( 8.14 ) можно записать и в другой форме:

x(t) = A₀ e^-nt sin (w₀^* t + a)                               ( 8.14a )

где

        – начальная ордината огибающей.

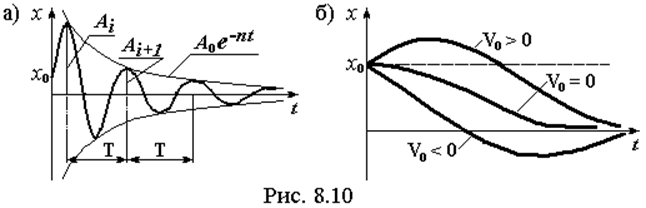Внешний вид решения ( 8.14 ) показан на рис. 8.10а. Это затухающая по экспоненте синусоида. Отношение двух последующих друг за другом амплитуд называется декрементом колебаний:

где T = 2p/w₀^*– период колебаний.

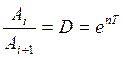Натуральный логарифм декремента колебаний называют логарифмическим декрементом колебаний:

L = lnD = nT

D и Lявляются мерой степени рассеяния энергии.

Если h> h_КР, то говорят, что система имеет “большое” демпфирование. В этом случае она уже не является колебательной и решение уравнения ( 8.12 ) имеет вид [ 12 ]:

( 8.15 )

где

Константы B₁ и B₂ определяются из начальных условий:

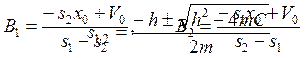Внешний вид решения ( 8.15 ) показан на рис. 8.10б. Это не колебательный процесс. В данном случае сила, создаваемая демпфером столь велика, что упругая сила может только вернуть массу m в исходное состояние.

8.7. Вынужденные  колебания  одномассовой  линейной системы

8.7.1. Виды  воздействий

Существует два вида внешних воздействий (рис. 8.11).

1. Силовое воздействие (рис. 8.11а), когда внешняя сила действует непосредственно на колеблющуюся массу. В этом случае возникают задачи ограничения амплитуды колебаний, ограничения перегрузок на массе, защиты окружающей среды, т.е. основания от вибрации.

2. Кинематическое воздействие (рис. 8.11б), когда колеблется основание. В этом случае возникают задачи защиты объекта (массы m): ограничения амплитуды ее колебаний, ограничения перегрузок.

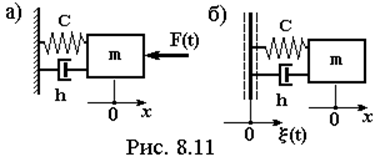Покажем, что с точки зрения математического описания эти два вида воздействия эквивалентны.

Уравнение движения массы при силовом воздействии по Принципу д’Аламбера:

m + h + Cx = F(t)                                  (  8.16 )

Уравнение движения массы при кинематическом воздействии:

m + h( – ) + C ( x– x(t)) = 0

Или

m + hx + Cx = + x(t)                                        (  8.17 )

Обозначив сумму в правой части уравнения ( 8.17 ) через F(t) приходим к уравнению в форме ( 8.16 ). Таким образом, все результаты, полученные для одного вида воздействия справедливы и для другого. В дальнейшем будем рассматривать главным образом силовое воздействие.

8.7.2. Режимы работы. Амплитудно-частотная характеристика.

Рассмотрим самый простой случай – колебаний массы m (рис. 8.11а) под действием внешней силы, изменяющейся по гармоническому закону. Уравнение движения в этом случае:

m + h + Cx = F₀cospt                              ( 8.18 )

Это обыкновенное, линейное, неоднородное дифференциальное уравнение. Из курса высшей математики известно, что его решение:

x(t) = x_ОРО(t) + x_ЧРН(t)

где x_ОРО(t) – общее решение однородного уравнения,

x_ЧРН(t) – частное решение неоднородного.

Однородное уравнение – это в данном случае уравнение, описывающее свободные колебания. Как показано выше – это затухающая со временем функция. Т.е. для любой системы существует промежуток времени, по истечении которого значения функции x_ОРО(t) становятся пренебрежимо малыми и остается только x_ЧРН(t). такие колебания называются установившимися или чисто вынужденными.

Частное решение неоднородного линейного дифференциального уравнения ищется в форме правой части, т.е.

x_ЧРН(t) = x(t) = A cos (pt + a)                                ( 8.19 )

Более удобной формой в данном случае будет

x(t) = D₁ cos pt + D₂ sin pt                                     ( 8.20 )

Найдем зависимость амплитуды колебаний A от частоты вынуждающей силы p. Для этого дважды продифференцируем выражение ( 8.20 ). С учетом того, что частота p постоянна получаем:

(t) = – p D₁sinpt + pD₂cospt

(t) = – p² D₁ cos pt – p²D₂ sin pt

Выражение ( 8.20 ) и производные подставим в уравнение ( 8.18 )

– m p² D₁ cos pt – m p²D₂ sin pt – h p D₁ sin pt + h pD₂ cos pt +

+ C D₁ cos pt + C D₂ sin pt = F₀ cos pt

Приравниваем коэффициенты при косинусах и синусах

– m p² D₁ + h pD₂  + C D₁ = F₀