Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 40

Из условия (7.5) получаем формулу для вычисления приведенного момента:

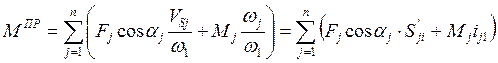
( 7.6 )

где S’_j1, i_j1 – передаточные функции и передаточные отношения.

Если звено приведения совершает поступательное движение, то для него вычисляют приведенную силу, выражение для которой получается аналогично:

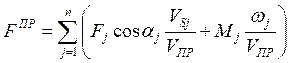
( 7.7 )

гдеV_ПР  – скорость звена приведения.

Подчеркнем еще раз, что по выражениям (7.6), (7.7) вычисляется приведенный момент или приведенная сила от всех сил и моментов, действующих на все звенья машины.

Рассмотрим важный частный случай: приведенный момент при известном КПД механизма. Эта задача часто встречается, например, при силовом расчете зубчатых механизмов. В п. 5.9.1 соответствующие формулы были даны без вывода. Теперь их можно получить строго.

Обозначим: N_S^* – мощность всех внешних сил за исключением сил трения. При известном КПД механизма h:

N_S = N_S^* / h

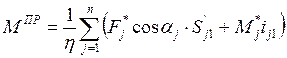Тогда из формулы (7.6) получаем:

( 7.8 )

где F_j^*, M_j^* – главные векторы и главные моменты сил, при вычислении которых не учитывались силы трения.

Если приводится только один момент, то из формулы (7.8) получаем:

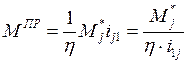
( 7.9 )

что соответствует выражениям, использовавшимся в подразделе 5.9.

7.4. Приведение  масс  и  моментов  инерции

Задача состоит в том, чтобы найти такой приведенный параметр, который эквивалентно включал в себя все инерционные свойства всех звеньев машины.

Мерой инертности тела в поступательном движении является его масса, а во вращательном – момент инерции. Поэтому, если звено приведения вращается, то в качестве приведенного параметра ищут приведенный момент инерции J^ПР, а если звено приведения движется поступательно – то приведенную массу m^ПР. Рассмотрим случай с вращающимся звеном приведения.

Условием приведения масс и моментов инерции к звену приведения является равенство кинетических энергий, которой суммарно обладают все звенья, входящие в машину и кинетической энергии звена приведения, т.е.:

E^ПР = E_S                                                    ( 7.10 )

Раскрывая выражения для кинетических энергий, имеем:

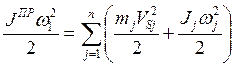
( 7.11 )

где m_j, J_j – массы и моменты инерции звеньев,

V_Sj  – скорости центров масс звеньев, w_j  – угловые скорости звеньев,

n – количество подвижных звеньев в машине.

Из условия (7.11) получаем формулу для вычисления приведенного момента инерции:

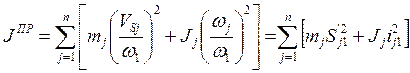
( 7.12 )

где S’_j1, i_j1 – передаточные функции и передаточные отношения.

Если звено приведения совершает поступательное движение, то для него вычисляют приведенную массу, выражение для которой получается аналогично:

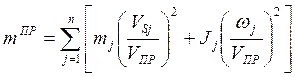
( 7.13 )

7.5. Уравнение  движения

Операции, проведенные в подразделах 7.3, 7.4 позволили сформировать динамическую модель, изображенную на рис. 7.2. Составим соответствующую математическую модель – уравнение движения звена приведения. Для этого воспользуемся Принципом виртуальных перемещений, из которого следует, что приращение кинетической энергии системы равно приращению работы внешних сил:

dE = dA_ВН

Раскрывая выражения для дифференциала кинетической энергии, и дифференциала работы для вращающегося звена приведения получаем:

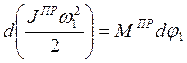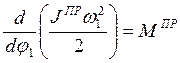или

( 7.14 )

Рассмотрим производную в левой части выражения ( 7.14 ).

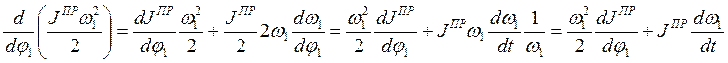Подставляя этот результат в выражение (7.14) получаем уравнение движения звена приведения в дифференциальной форме:

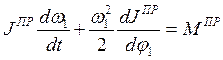
( 7.15 )

7.6. Анализ  уравнения  движения

Преобразуем уравнение движения (7.15). Приведенный момент в правой части обычно для удобства представляют в виде двух слагаемых: M_Д^ПР – приведенный момент сил движущих, M_С^ПР – приведенный момент сил сопротивления.

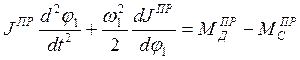
( 7.16 )

Такое разделение вызвано тем, что эти моменты обычно зависят от разных параметров. Например, для машин, приводящихся в движение асинхронными электродвигателями, движущий момент M_Д ими развиваемый, а следовательно и M_Д^ПР является функцией угловой скорости: M_Д = f(w_Д), M_Д^ПР = f(w₁). Силы сопротивления, например, у технологических машин обычно зависят от положения, т.е. M_C^ПР = f(j₁). Возможны и другие  случаи.

Рассмотрим физический смысл слагаемых в левой части уравнения (7.16). Первое слагаемое представляет собой инерционный момент, действующий на тело, имеющее угловое ускорение: