Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 23

4.8.1. Механизмы  с  толкателем  и  роликом

или  с  заостренным  толкателем

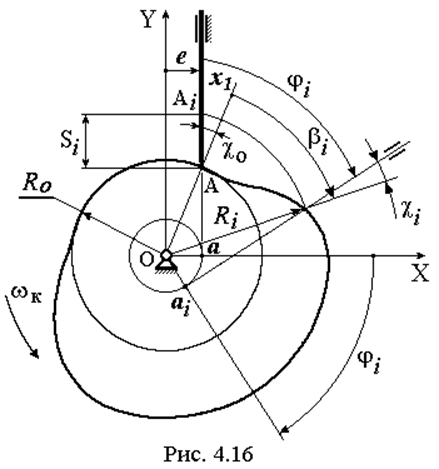
Расчет начинаетсяс построения центрового профиля (рис. 4.16), т.е. траектории точки А – центра ролика на вращающейся плоскости кулачка, что выполняется  методом  инверсии (обращенного  движения) [ 1, 5, 14, 18 ].

Если за полярную ось x₁ принять прямую ОА, то формулы для полярных координат (R_i, b_i) в i-м положении механизма (j = j_i) легко получаются из схемы  на  рис. 4.16  [ 5, 9 ]:

b_i  = j_i–(c_i –c_o),

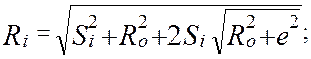
где c_i = arcsin(e/R_i), c_o= arcsin(e/Ro).

В формулах ( 4.29 ) автоматически учитывается знак эксцентриситета e. Направление отсчета углов противоположно направлению вращения кулачка. Произведя вычисления по формулам ( 4.29 ) для i = 1, 2, . . . n, получаем  координаты  всего  центрового  профиля.

Рабочие профили (рис. 4.17) получаются как огибающие семейства окружностей радиусом ролика Rp с центрами на центровом профиле Ц. Радиус-вектор R_1i рабочего профиля P₁ определяется из треугольника OA_iB по теореме  косинусов

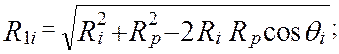( 4.30 )

где q_i = arcsin (S’_icos g _i /R_i).

Полярный  угол  вектора  R_1i  в  обращенном  движении:

b_1i = b_i + q_1i – q_i,                                                      ( 4.31 )

где q_1i = arcsin (S’_icos g _i /R_1i).

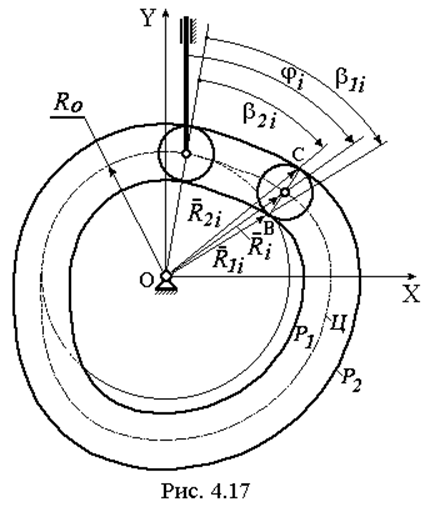Для механизмов с геометрическим замыканием радиус-вектор второго рабочего профиля P₂ определяется из треугольника ОВС:

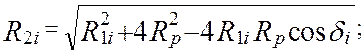                          ( 4.32 )

где  d_i =  p –ïq_i ê–ïq_1i – q_i÷.

Полярный  угол  вектора  R_2i  в  обращенном  движении:

b_2i= b_1i ± ïarcsin(2Rp sind_i /R_2i)ï.                             ( 4.33 )

Знак плюс берется для фазы возврата, знак минус – для фазы удаления.

4.8.2. Механизмы  с  плоским  толкателем

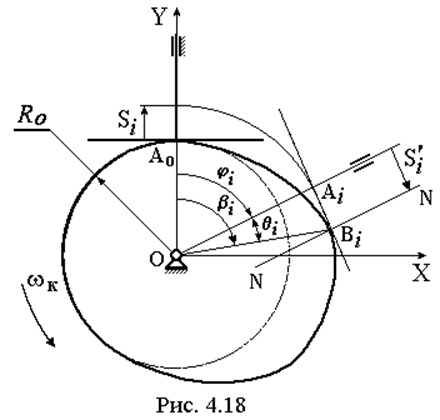
Расчетная схема для построения профиля кулачка механизма данного типа методом инверсии представлена на рис. 4.18. Точка контакта кулачка и толкателя перемещается по его рабочей поверхности. Для любого i-го положения (j = j_i)  радиус-вектор  профиля  кулачка  [ 5 ]:

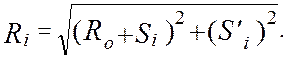                                  ( 4.34 )

Полярный  угол  вектора  R_i  в  обращенном  движении

b_i = j_i + q_i,                                                     ( 4.35 )

где q_i – угол подъема между радиусом-вектором R_i и нормалью  N-N:

tgq_i = S’_i /(R_i+ S_i )                                             ( 4.36 )

Произведя вычисления по формулам ( 4.34 ) … ( 4.36 ) для i = 1, 2, . . . n, получаем  координаты  всего  профиля.

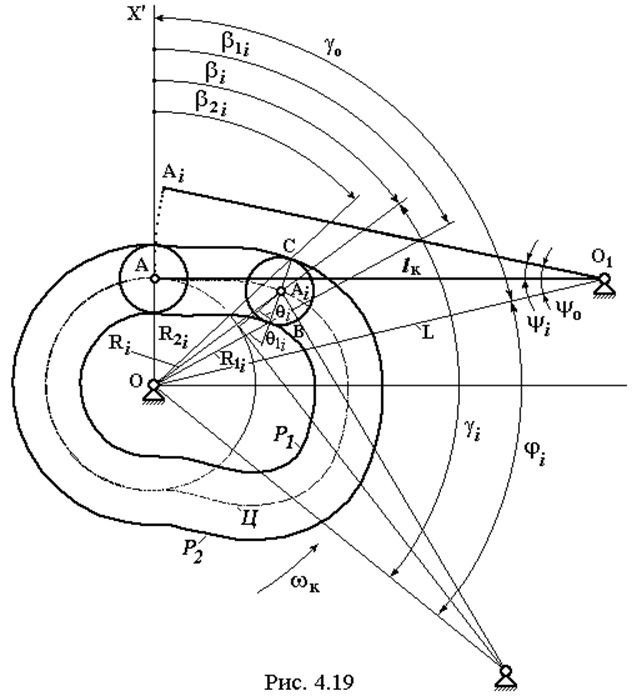
4.8.3. Механизмы  с  коромыслом  и  роликом

Расчетная схема для построения профиля кулачка механизма данного типа методом инверсии представлена на рис. 4.19. Здесь, как и для механизма с толкателем, расчет профиля кулачка начинается с построения его центрового профиля Ц, т.е. траектории точки A в обращенном движении. Полярные координаты центрового профиля (R_i, b_i) относительно оси X’ для i-го положения (j = j_i) вычисляются по формулам [ 5, 9 ][2]:

где y_i  – угол поворота коромысла O₁A в положении;

y₀  = arccos[(L² + l_к² – R₀²) / (2 L l_к)] – угол, характеризующий начальное положение коромысла;

g₀  = arccos[(R₀² + L² – l_к²) / (2 R₀ l_к)];

g_i  = arccos[(R_i ² + L² – l_к²) / (2 R_i l_к)].

При расчете угла b_i  знак плюс берется, если на фазе удаления направления вращения кулачка и коромысла противоположны (см. рис. 4.19), и знак минус – если одинаковы. Произведя расчеты по формулам ( 4.37 ) для i = 1, 2, . . . n, получаем координаты центрового профиля кулачка для всего профилируемого участка.

Радиус-вектор R_1i рабочего профиля P₁ определяется из треугольника OA_iB по теореме косинусов:

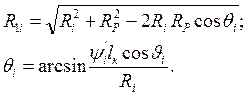
( 4.38 )

где R_P  – радиус ролика.

Полярный угол, для которого вычислен R_1i в обращенном движении:

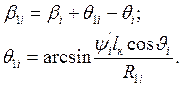
( 4.39 )

Для механизма с геометрическим замыканием полярные координаты точки C второго рабочего профиля P₂ определяется из треугольника OBC по формулам ( 4.32 ), ( 4.33 ).

4.8.4. Определение радиуса ролика