 По данной классификации структурной группе
приписывают класс и порядок. Классом структурной группы считается количество
кинематических пар во внутреннем контуре группы. Порядком структурной группы
считается количество кинематических пар, которыми она присоединяется к
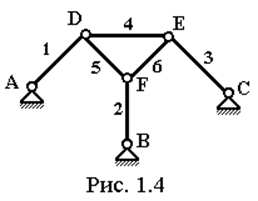
остальному механизму. На рис. 1.4 дан пример структурной группы 3-го класса
3-го порядка. Здесь звенья 4, 5, 6 образуют внутренний контур, в котором три
кинематические пары. К остальному механизму данная группа присоединяется тремя
шарнирами: A, B, C.
По данной классификации структурной группе
приписывают класс и порядок. Классом структурной группы считается количество
кинематических пар во внутреннем контуре группы. Порядком структурной группы
считается количество кинематических пар, которыми она присоединяется к
остальному механизму. На рис. 1.4 дан пример структурной группы 3-го класса
3-го порядка. Здесь звенья 4, 5, 6 образуют внутренний контур, в котором три
кинематические пары. К остальному механизму данная группа присоединяется тремя
шарнирами: A, B, C.
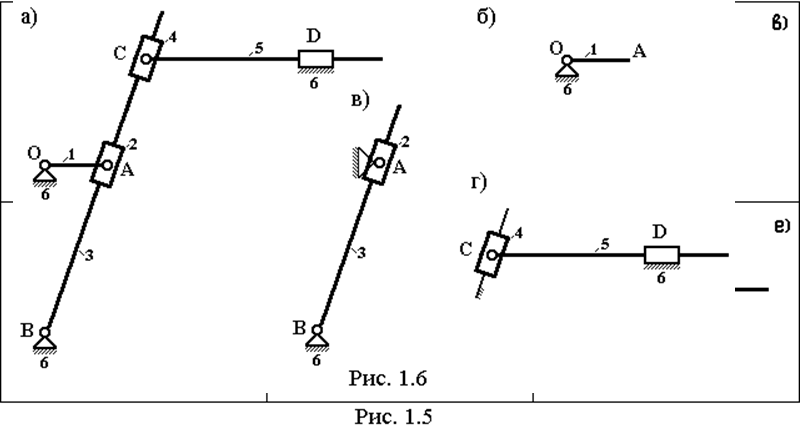
К недостаткам данной классификации можно отнести то, что структурные группы, которым приписывается 2-й класс, 2-й порядок не имеют ярко выраженного признака второго класса. На рис. 1.5 показаны все виды таких групп.
К механизму эти группы присоединяются следующим образом: кинематической парой A – всегда к подвижному звену, кинематическая пара C (рис. 1.5а) или B (рис. 1.5б,в,г,д,е) – может осуществлять соединение со стойкой или другим подвижным звеном.
 |
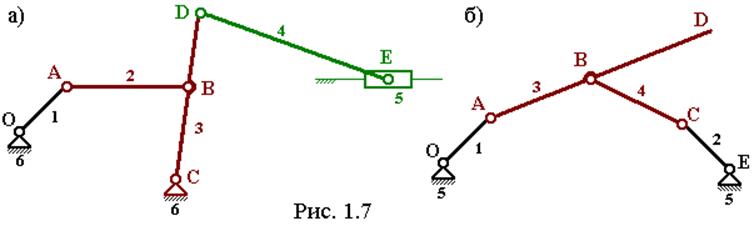
На рис. 1.6 дан пример структурного анализа механизма. На рис. 1.6а изображен шестизвенный, плоский рычажный механизм, а на рис. 1.6б,в,г – его структурное деление на входное звено кривошип ОА (рис. 1.6б) имеющее число степеней свободы W = 1 и две структурные группы 2-го класса, 2-го порядка (рис. 1.6в,г).
1.4. Структурный синтез механизмов с помощью групп Ассура
 |
1.5. Диагностика наличия пассивных связей
При формировании механизма из структурных групп вопрос о наличии пассивных связей в механизме не возникает. Но он может возникнуть при анализе уже существующих механизмов или нарисованных “от руки”, например, заказчиком.
Алгоритм диагностики пассивных связей основан на анализе матрицы смежности механизма, которая представляет собой квадратную таблицу с количеством строк и столбцов, равным числу звеньев, включая стойки.
Матрица смежности формируется следующим образом. В каждой ее ячейке с индексами “i”, “j”, где i – номер строки, j – номер столбца, ставится “0”, если i-е и j-е звенья не образуют кинематической пары. Если же они образуют кинематическую пару, то ставится цифра, равная числу степеней свободы этой кинематической пары.
Рассмотрим “классический” пример механизма с пассивной связью (см. рис. 1.3). Составим для него матрицу смежности (табл. 1.1, нули опущены).
|
N |
1 |
2 |
3 |
4 |
5 |
|
1 |
- |
1 |
1 |
1 |
|
|
2 |
1 |
- |
1 |
||
|
3 |
1 |
- |
1 |
1 |
|
|
4 |
1 |
1 |
- |
||
|
5 |
1 |
1 |
- |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.