Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 25

Следствия из основной теоремы зацепления. Для того чтобы передаточное отношение было постоянным необходимо, чтобы в процессе зацепления полюс зацепления не менял своего положения.

В свою очередь для того, чтобы полюс зацепления не менял своего положения необходимо, чтобы профили контактирующих поверхностей представляли собой взаимоогибаемые кривые.

В полной мере этому требованию удовлетворяют циклоиды (см. рис. 5.2б), которые образуются при перекатывании без скольжения одной окружности по другой. И исторически первым правильным зацеплением было именно циклоидальное, т.е. такое, когда боковые поверхности зубьев представляют собой отрезки циклоид.

Однако у циклоидального зацепления есть недостаток – его сравнительно высокая стоимость. Причины этого рассматриваются позже в подразделе “Методы изготовления зубчатых колес”.

Требованию основной теоремы зацепления удовлетворяет и эвольвента окружности – кривая, образующаяся при перекатывании без скольжения прямой по окружности (см. рис. 5.2в). Изготовление колес с эвольвентным профилем зубьев оказалось гораздо более дешевым, и, несмотря на то, что такие колеса имеют несколько большие размеры, – эвольвентное зацепление в машиностроении получило самое широкое применение. В дальнейшем рассматривается именно этот вид зацепления.

5.3. Основные параметры эвольвентного зацепления

Одна из характерных окружностей зубчатого колеса фактически уже была определена – это основная окружность, диаметр которой обозначается d_b (см. рис. 5.2в) – это окружность, разверткой которой и образуется эвольвента.

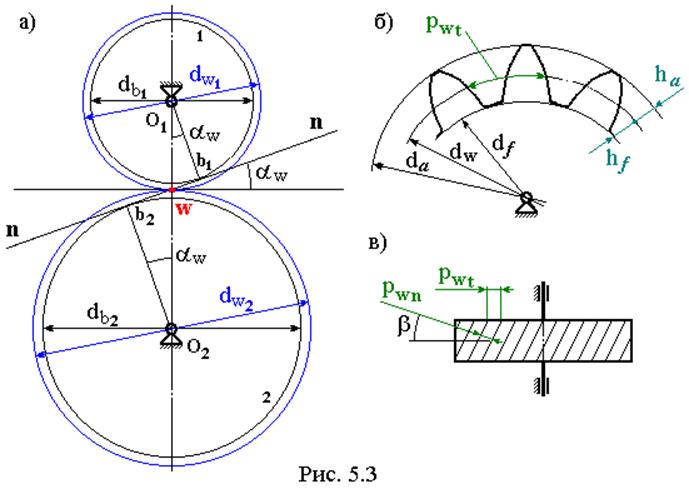
На рис. 5.3а представлена схема зацепления двух колес. Окружности, проведенные из центров вращения колес через полюс зацепления, называются начальными и обозначаются d_W (все обозначения параметров стандартизованы).

При эвольвентном зацеплении требование теоремы Виллиса выполняется “с избытком”. В данном случае не только полюс зацепления неподвижен, но в процессе всего зацепления неподвижна вся общая нормаль к контактирующим поверхностям n-n. По способу образования эвольвенты очевидно, что общая нормаль является касательной к основным окружностям обоих колес и радиусы этих окружностей определяются перпендикулярами O₁b₁, O₂b₂.

Угол между касательной к начальным окружностям колес и нормалью к контактирующим поверхностям n-n называется углом зацепления a_W.

Соотношение между диаметром начальной и основной окружности:

d_b = d_W cos a_W                                                ( 5.2 )

Шагом зацепления называется расстояние между одноименными точками профилей двух соседних зубьев (см. рис. 5.3б). Шаг измеряют по дуге начальной или основной окружности. В первом случае его обозначают p_W, а во втором – p_b. Для косозубых и винтовых колес шаг можно измерять по торцу зуба (см. рис. 5.3в), тогда шаг называют торцевым и в индексе ставят значок “t” или по нормали к оси зуба, в этом случае его называют нормальным и в индексе ставят значок “n”. В соответствии с выражением ( 5.2 ):

p_b = p_W cos a_W                                                    ( 5.3 )

Нормальный шаг:

p_n = p_t cos b                                                      ( 5.4 )

где b – угол наклона зубьев косозубого колеса (см. рис. 5.3в).

Важнейшим параметром любого зубчатого колеса является его модуль. По определению модуль зубчатого колеса это:

m = p_Wt / p;                                                      ( 5.4 )

Подчеркнем, что выражение ( 5.5 ) – это определение понятия “модуль зубчатого колеса”, а не формула для его вычисления. В дальнейшем мы узнаем, что “m” определяется по условиям прочности или точности.

Понятие модуля колеса важно в первую очередь тем, что любой размер зубчатого колеса выражают в виде некоторого безразмерного коэффициента  умноженного на “m”, или комбинации коэффициентов, умноженной на “m”. Это позволяет унифицировать проектные расчеты.

Величины модулей зубчатых колес стандартизованы, т.е. в ГОСТах перечислены те значения “m”, которые допускается применять при проектировании.