Fh = Fh0 Sign 
( 8.9 )
Третью гипотезу, которую мы здесь упомянем, это гипотеза аэродинамического трения, в соответствии с которой предполагают, что сила, создаваемая демпфирующим элементом пропорциональна квадрату скорости деформации:
Fh = h 2 (
8.10 )
Введение в динамическую модель отдельного демпфирующего элемента не единственный способ учета рассеяния энергии. Более точными, но и гораздо более сложными являются модели, в которых упругие и демпфирующие свойства рассматриваются в рамках единой упруго-демпфирующей связи. При этом сила, ею создаваемая обычно рассматривается как некоторая единая функция
FCh = f(x,
)
Одним из таких способов является гипотеза гистерезиса. В соответствии с ней считается, что характеристики связи различны при ее нагружении и разгружении. Если учесть силы неупругого сопротивления, направление которых противоположно скорости деформации, непосредственно в характеристике FC(x), то она будет иметь две ветви (рис. 8.9,а), верхняя будет соответствовать нагружению связи, а нижняя – разгружению. Так образуется фигура, называемая петлёй
 |
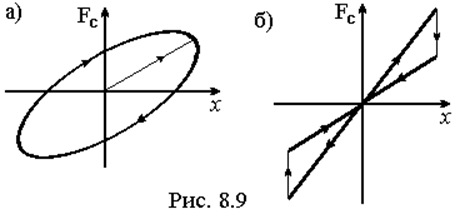При всех преимуществах такого описания связи есть один большой недостаток. Для расчета параметров петли гистерезиса надо знать амплитуду колебаний, а она становится известной только после расчета процесса. Этот недостаток еще можно преодолеть организацией итерационного процесса последовательных приближений, но он дает результат только для установившихся колебаний достаточно простой формы. Для расчета нестационарных колебательных процессов практическое применение такой методики натыкается на значительные трудности.
Есть один частный случай петли гистерезиса, свободный от указанных недостатков. Это петля, показанная на рис. 8.9,б. Фактически, такая силовая характеристика соответствует предположению о скачкообразном изменении коэффициента жесткости при переходе от нагружения связи к ее разгружению (гипотеза Корчинского). Для практических расчетов такая зависимость удобна, но и она имеет существенный недостаток: при моделировании с ее помощью движения объекта на графике ускорения появляются скачки ускорения, не наблюдающиеся в экспериментах.
В дальнейшем мы ограничимся рассмотрением только самого простого случая, соответствующего схеме Кельвина-Фойхта, с использованием гипотезы вязкого трения.
8.6. Собственные колебания одномассовой
линейной диссипативной системы
На рис. 8.8,а показана линейная одномассовая колебательная система по схеме Кельвина-Фойхта, с использованием гипотезы вязкого трения.
Уравнение ее движения запишем на основании Принципа д’Аламбера. При одномерных собственных колебаниях на массу m действует только три силы: две силы со стороны упругого элемента и сила инерции:
FC + Fh = FИ
где FC – сила, создаваемая упругим элементом, Fh – сила, создаваемая демпфирующим элементом, FИ – сила инерции.
Раскрывая выражения для сил, получаем:Cx + h = – m
Или в более привычной записи
m + h + Cx = 0 ( 8.11 )
Деля на массу, получаем
+ 2n + w02x = 0 ( 8.12 )
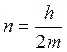где
– коэффициент затухания.
Решение уравнения (8.12) зависит от соотношения коэффициентов.
Существует значение критического демпфирования:
( 8.13 )
Колебательной система является если h < hКР. В этом случае говорят, что система имеет “малое” демпфирование и решение уравнения (8.1 ) имеет вид [12]:
x(t) =e-nt (B1 cos w0* t + B2 sin w0* t) ( 8.14 )
где
– частота собственных затухающих колебаний.
Константы B1 и B2 находят из начальных условий. Пусть x(0)= x0, (0)= V0. Тогда из выражения ( 8.14 ) при t = 0 имеем
B1 = x0
Дифференцируем выражение ( 8.14 ) по времени
(t) = –n e-nt (B1 cos w0* t + B2 sin w0* t) + e-nt (–B1 w0* sin w0* t + B2 w0* cos w0* t)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.