Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 16

     e₂ (t) = e_m e*(t),                                                       ( 4.1 )

где  e_m – неизвестная  пока  амплитуда.

Дважды интегрируя выражение ( 4.1 ), получим:

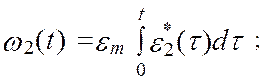
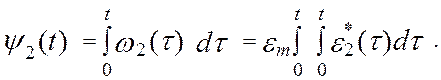
Интегрирование производится с начальными условиями: для фазы удаления w₂(t) = 0, y₂(t) = 0; для фазы возврата w₂(t) = 0, y₂(t) = y_m. Максимальное перемещение выходного звена y_m известно, поэтому амплитуда  ускорения

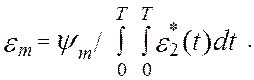
Каждому значению функций  y₂(t), w₂(t), e₂(t) могут быть поставлены в соответствие величины y₂(j), w₂(j), e₂(j), которые и используются для проектирования  механизма,  как  это  описано  ниже.

Следует заметить, что существует идругая причина возникновения ударов в кулачковых механизмах, связанная с динамикой их работы. Кулачок может быть спроектирован и безударным, в том смысле, какой мы вкладывали в это понятие выше. Но на больших скоростях у механизмов с силовым замыканием возможен отрыв толкателя (коромысла) от кулачка. Через какое-то время замыкающая сила восстанавливает контакт, но это восстановление и происходит с ударом. Такие явления могут возникать, например, когда фаза возврата задана слишком маленькой. Профиль кулачка тогда на этой фазе получается крутым и по окончании фазы дальнего выстоя замыкающая сила не успевает обеспечить контакт и толкатель как бы срывается с профиля кулачка на дальнем выстое и может даже сразу ударить в какую-то точку кулачка на ближнем выстое. У механизмов с геометрическим замыканием ролик движется по пазу в кулачке. Поскольку между роликом и стенками паза обязательно есть зазор, то в процессе работы ролик ударяется о стенки, интенсивность этих ударов тоже возрастает с увеличением скорости вращения кулачка. Для изучения этих явлений необходимо составлять математическую модель работы всего механизма,  но эти  вопросы  выходят  за  рамки  данного  курса.

4.4.2. Функциональные  механизмы

Поскольку эти механизмы проектируются для воспроизведения требуемой функции перемещения выходного звена, следовательно, функцию S(j) или y(j) можно считать заданной. Дифференцируя эти зависимости, получают функции скорости и ускорения выходного звена, которые и используются для проектирования  механизма,  как  это  описано  ниже.

Заметим, однако, что операция дифференцирования чувствительна к погрешностям в значениях функции. Если закон перемещения задан аналитически, то проблем с дифференцированием не возникает. Но если он задается таблицей значений, да еще может быть полученной экспериментально, то, как правило, требуется применение специальных методов, позволяющих уменьшить  погрешности.

В частности, если такая таблица получена экспериментально, то обычно требуется произвести ее сглаживание. Это можно сделать, например, с помощью сглаживающих сплайнов [ 6, 7, 15 ] или путем фильтрации [ 3, 11 ]. В указанной литературе рассматриваются отнюдь не кулачковые механизмы, но проблема сглаживания функций носит общий характер.

Сам процесс дифференцирования функций, заданных таблично имеет “подводные камни”. Как правило, требуется применение комбинированных методов. Например, если функция имеет участки с различным характером изменения, то на линейных участках надо применять обычный метод трапеций, а на криволинейных эффективно использование интерполяционных сплайнов. Методика такого дифференцирования описана  в  работе [ 15 ].

4.5. Угол давления в кулачковых механизмах

Углом давления в кинематической паре называется угол между вектором реакции со стороны ведущего звена на ведомое, и вектором скорости точки контакта, если считать эту точку принадлежащей ведомому звену. Это определение справедливо для любой кинематической пары.

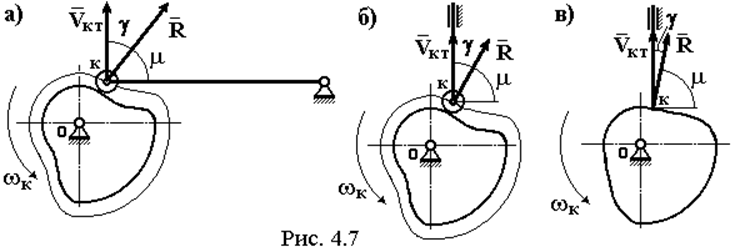На рис. 4.7 показан угол давления g для кинематических пар между кулачком и толкателем для различных типов механизмов с роликовым контактом и заостренным толкателем. Здесь мы будем рассматривать только такие механизмы, ввиду того, что для механизмов с плоским толкателем рассматриваемый вопрос не актуален, т.к. у таких механизмов угол давления в кинематической паре кулачок-толкатель всегда g= 0.