Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 8

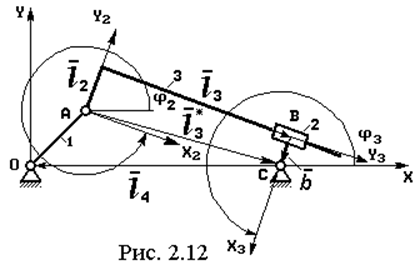
Механизмы двух модификаций, состоящие из входного звена OA и структурных  групп с кулисами  представлены на рис. 2.11, 2.12. Ось кулисы в общем случае может быть смещена как от шарнира A на величину l₂, так и от опоры B на величину b. Смещения на рисунках показаны положительными. Введем в рассмотрение вектор l₃^* из точки A в точку B, который соответствует положению кулисы при отсутствии смещений. Найдем сначала решение для этого случая (все величины, помеченные ниже звездочкой  относятся к случаю l₂ = b = 0).

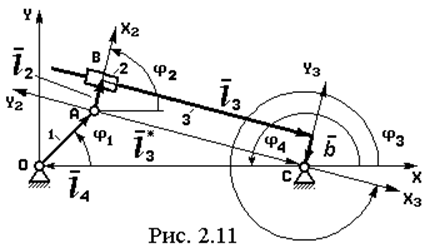
Если занумеровать звенья так, как это показано на рис. 2.11, 2.12, то уравнение замкнутого векторного контура для обеих модификаций запишется одинаково:

-       -       -

l₁  +  l₃^* +  l₄  = 0 .

Проецируя его на оси неподвижной системы координат OXY и учитывая, что

j₄  = 180^О = Const, а  l₁cos j₁ = x_A,   l₁ sin j₁ = y_A – координаты входного шарнира  A,  получим:

x_A +  l₃^* cos j₃^*  –  l₄  = 0;

y_A +  l₃^* sin j₃^*  = 0.

Из системы ( 2.23 ) находим:

 

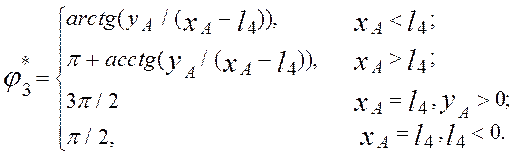
( 2.24 )

 

 

 

 

 

 

 

Отметим, что при вычислении по формулам ( 2.24 ) результат l₃^* = 0 является признаком неработоспособности механизма если в процессе движения входное звено должно проходить положение ( x_A = l₄ , y_A = 0 ).

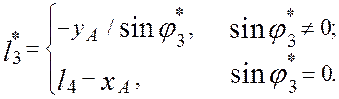
Для определения угловой скорости кулисы  w₃^*  и скорости ползуна относительно кулисы V₃^* продифференцируем систему ( 2.23 ) по времени:

V_Ax + V₃^* cos j₃^*  –  l₃ w₃^* sin j₃^*  = 0 ;

V_Ay + V₃^* sin j₃^*  +  l₃ w₃^* cos j₃^*  =  0.

где: V_Ax,V_Ay – проекции скорости входного шарнира A (см. уравнения ( 2.20 ).

Система ( 2.25 ) линейна относительно w₃^*, V₃^*  т.е. легко разрешима, например, по формулам Крамера.

Дифференцируя ( 2.25 ) по времени, получим систему уравнений для определения углового ускорения кулисы e₃^* и ускорения ползуна относительно  кулисы  a₃^*:

a_Ax+a₃^* cosj₃^* – 2V₃^* w₃^* sinj₃^* – l₃^* e₃^* sinj₃^* – l₃^* w₃^*2 cosj₃^* = 0;

a_Ay+a₃^* sinj₃^*+ 2V₃^* w₃^* cosj₃^* + l₃^* e₃^* cosj₃^* – l₃^*w₃^*2 sinj₃^*= 0.

где:  a_Ax, a_Ay– проекции ускорения входного шарнира  A  на  оси  неподвижной  системы  координат  OXY ( см. уравнение ( 2.16 ).

Кинематические параметры движения кулисы при наличии смещений l₂, b (см. рис.  2.11, 2.12)  получим через параметры движения вектора l₃^*, который  повернут  относительно  вектора  l₃  на  угол ¡ :

¡  = arcsin((b – l₂ )/l₃^* );      j₃  = j₃^*  + ¡ ;       l₃  = l₃^* cos ¡ .                ( 2.27 )

На рис. 2.11, 2.12 показаны положительные смещения  l₂ и b.

Дифференцируем  дважды  по  времени  выражения  для  j₃  и  l₃:

.                           ..

w₃  = w₃^*  + ¡ ;      e₃  = e₃^*  + ¡ ;

.

V₃  = V ₃^* cos ¡ –  l₃^* ¡ sin ¡ ;                                                                 ( 2.28 )

.                    ..              .

a₃  = a₃^* cos ¡  – 2 V₃^* ¡ sin ¡  –  l₃^*(¡ sin ¡ + ¡² cos ¡ ),

Необходимые для вычисления по формулам ( 2.28 ) производные от ¡, определим  последовательно  дифференцируя  первое  из  выражений ( 2.27 ):

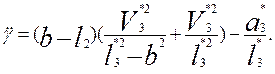
2.4. Метод  преобразования  координат

Во всех рассмотренных выше задачах выбиралась такая система координат OXY, в которой уравнения кинематики имеют наиболее простой и удобный для решения вид. Однако конечный результат часто бывает необходимо получить в некоторой неподвижной системе координат, в которой рассматривается весь механизм в целом. Кроме того, полученные в подразделе 2.3 выражения не позволяют определять кинематические параметры движения произвольных точек на звеньях механизмов, например, центров масс, рабочих органов и т.п. Все эти проблемы удобно решать методом  преобразования  координат.

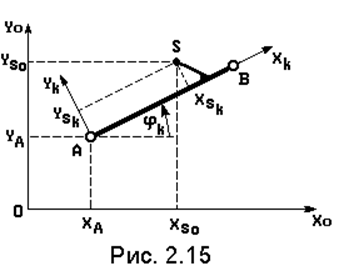
Рассмотрим данный метод в общем виде. Пусть АВ (рис. 2.15) некоторое k-е звено механизма и требуется определить кинематическое параметры движения точки “S” этого звена с неподвижной системе координат  (НСК)  OXoYo.