Уравнение равновесия всей структурной группы в
целом:
![]() (3.11)
(3.11)
Здесь четыре неизвестных ![]() . Касательные
составляющие найдем, рассматривая отдельно равновесия звеньев.
. Касательные
составляющие найдем, рассматривая отдельно равновесия звеньев.
Равновесие звена 2 в виде равенства нулю суммы всех моментов относительно точки B1:
R12t×lAB = 0
показывает, что при принятых допущениях R12t = 0.
Равновесие звена 3 в виде равенства нулю суммы всех моментов относительно точки B1:
R63t×lBC + R43×h43 = 0
позволяет определить величину R63t. Длину плеча h43 можно замерить на выполненной в масштабе расчетной схеме.
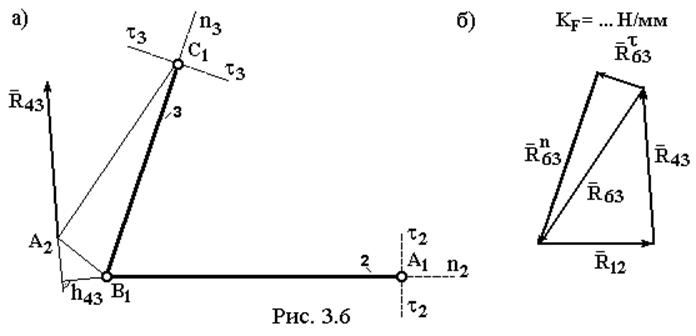
Теперь уравнение равновесия (3.11) можно решить графически путем построения плана сил (см. рис. 3.6,б).
План сил представляет собой графическое изображение уравнения равновесия. Сначала в выбранном масштабе KF отложите известные силы R43 и R63t. Потом замкните план, проведя линии действия R63n и R12n.
Примечание. Силовой расчет этой структурной группы рассмотрен на примере схемы 3 главного механизма. Для схемы 1, в которой совпадают точки B1 и A2 R63t = 0 и план сил упрощается до треугольника. В схеме 2 точки B1 и A2 не совпадают, но расположены иначе, R63t ¹ 0 и все выкладки аналогичны, но план сил имеет несколько другую конфигурацию.
3.3.2. Силовой расчет кривошипа
В отличие от рассмотренных выше структурных групп, кривошип отдельно взятый имеет число степеней свободы W = 1. Поэтому сам по себе он не является уравновешенной системой. Его силовой расчет надо рассматривать в более широком контексте – вместе с силами, приводящими его в движение.
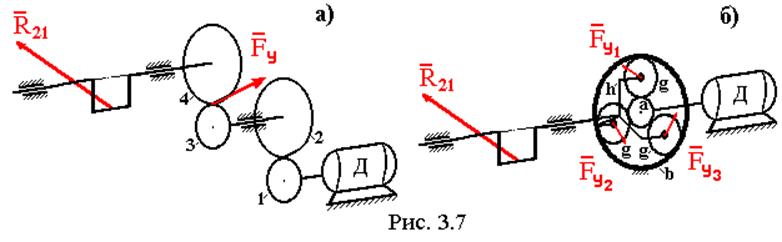
Тип силового расчета кривошипа зависит от того, как передается крутящий момент с вала двигателя на вал кривошипа. На рис. 3.7 показаны два варианта, рис. 3.7,а – момент передается через рядный двухступенчатый зубчатый редуктор, рис. 3.7,б – момент передается через планетарный зубчатый редуктор схемы A.
Силовой расчет кривошипа при передаче
крутящего момента
через рядный зубчатый редуктор
Целью данного расчета является определение реакции в
опоре кривошипа ![]() . Расчетная схема показана на
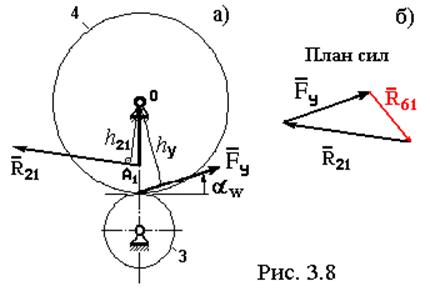
рис. 3.8,а. Она соответствует общей схеме, изображенной на рис. 3.7,а. Здесь
. Расчетная схема показана на
рис. 3.8,а. Она соответствует общей схеме, изображенной на рис. 3.7,а. Здесь ![]() реакция со
стороны шатуна 2 на кривошип. Реакция
реакция со
стороны шатуна 2 на кривошип. Реакция ![]() , её
величина и направление были определены выше при силовом расчете
трехшарнирной структурной группы. FУ – уравновешивающая сила, по своему физическому смыслу
– это реакция в зацеплении колес 3-4, и именно эта сила вращает кривошип.
, её
величина и направление были определены выше при силовом расчете
трехшарнирной структурной группы. FУ – уравновешивающая сила, по своему физическому смыслу
– это реакция в зацеплении колес 3-4, и именно эта сила вращает кривошип. ![]() – угол зацепления. Все параметры зубчатых
колес определены при проектировании привода. Если расчетную схему (рис. 3.8,а)
выполнить в масштабе, с соблюдением направления сил, то плечи h21, hУ можно замерить прямо на
чертеже.
– угол зацепления. Все параметры зубчатых
колес определены при проектировании привода. Если расчетную схему (рис. 3.8,а)
выполнить в масштабе, с соблюдением направления сил, то плечи h21, hУ можно замерить прямо на
чертеже.
Рассмотрим случай, когда вес кривошипа G1 пренебрежимо мал по
сравнению с ![]() . Уравновешивающую силу найдем из условия
равновесия кривошипа в виде равенства нулю суммы моментов относительно точки O:
. Уравновешивающую силу найдем из условия
равновесия кривошипа в виде равенства нулю суммы моментов относительно точки O:
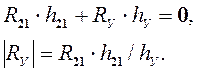
Тогда уравнение равновесия кривошипа:
![]() (3.12)
(3.12)
Уравнение (3.12) решим графически, путем построения
плана сил (рис. 3.8,б). Векторы ![]() и
и ![]() откладываем в масштабе с учетом
направления. Замыкая план, находим искомый вектор
откладываем в масштабе с учетом
направления. Замыкая план, находим искомый вектор ![]() .
Замеряя его на плане, и, умножая длину на масштабный коэффициент плана,
определяем величину реакции.
.
Замеряя его на плане, и, умножая длину на масштабный коэффициент плана,
определяем величину реакции.
Силовой расчет кривошипа при передаче крутящего момента
через планетарный зубчатый редуктор
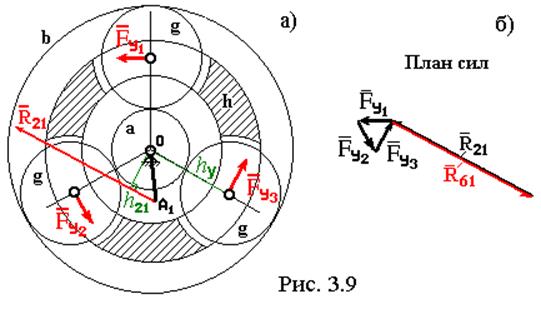
Целью данного расчета является определение
реакции в опоре кривошипа ![]() . Расчетная схема
показана на рис. 3.9,а. Она соответствует общей схеме, изображенной на рис.
3.7,б. Здесь
. Расчетная схема
показана на рис. 3.9,а. Она соответствует общей схеме, изображенной на рис.
3.7,б. Здесь ![]() реакция
со стороны шатуна 2 на кривошип. Реакция
реакция
со стороны шатуна 2 на кривошип. Реакция ![]() , её
величина и направление были определены выше при силовом расчете
трехшарнирной структурной группы. В данном случае действует несколько
уравновешивающих сил – столько, сколько сателлитов nW. На
расчетной схеме представлен случай nW = 3.
, её
величина и направление были определены выше при силовом расчете
трехшарнирной структурной группы. В данном случае действует несколько
уравновешивающих сил – столько, сколько сателлитов nW. На
расчетной схеме представлен случай nW = 3.
Все параметры зубчатых колес определены при проектировании привода. Если расчетную схему (рис. 3.9,а) выполнить в масштабе, с соблюдением направления сил, то плечо h21 можно замерить прямо на чертеже, а плечо действия уравновешивающих сил:
hУ = mag (Za + Zg)/2, где mag – модуль зубчатых колес, Za, Zg – числа зубьев колес.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.