Конспект лекций по дисциплине "Теория вероятностей и математическая статистика"

МИНИСТЕРСТВО  АГРАРНОЙ  ПОЛИТИКИ  УКРАИНЫ

КЕРЧЕСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра высшей математики и физики

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

КОНСПЕКТ ЛЕКЦИЙ

направления 6.090201 «Водные биоресурсы и аквакультура»

Керчь  2008 г.

Автор (составитель): Ершова Т.Г., ст. преподаватель кафедры высшей математики и физики КГМТУ

Конспект лекций рассмотрен и одобрен на заседании кафедры ВМ и Ф КГМТУ,

протокол №   10    от   « 12 »     06     2008 г.

          Керченский государственный морской технологический университет

 Функция нескольких переменных

(на примере функции двух переменных)

Рассмотрим плоскость ХОУ. Каждой паре чисел (х, у) можно поставить в соответствие точку М(х, у) на плоскости.

Определение  Если каждой паре значений двух независимых друг от друга переменных х и у из области D Ì ХОУ соответствует определенное значение величины z, то говорят, что z есть функция двух переменных х и у, определенная в области D, и пишут .

Областью определения D функции  называется совокупность тех пар значений (х, у), при которых z вычисляется конечным действительным числом (или определена, или существует).

Линия Г, ограничивающая область D, называется границей области.

Точки области D, не лежащие на границе Г, называются внутренними точками области D.

Область D, содержащая только внутренние точки, называется открытой (незамкнутой).

Если же D содержит и точки Г, то D называется замкнутой областью.

Область D называется ограниченной, если ее можно поместить в круг конечного радиуса с центром в начале координат.

Следовательно, область определения функции  есть часть плоскости ХОУ или вся плоскость.

Примеры:  1) . о.о.ф. D есть плоскость ХОУ.

2) ;   ;   . Граничная линия Г: .

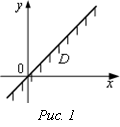
Возьмем пробную точку А(-1; 1) Ï Г. Подставим ее координаты в неравенство ;  , получили неверное числовое неравенство. Заштрихуем нижнюю полуплоскость – это и есть D. Г Î D, следовательно, D – замкнутая неограниченная область

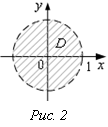
3) ;  ;  . Граничная линия: . Пробная  т.О(0,0): ,  верное числовое неравенство, заштрихуем внутренность круга, это и есть D – открытая, ограниченная область.

Пусть дана  и ее область определения D. В каждой точке М(х, у) Î D восстановим перпендикуляр, равный по величине значению . В пространстве получим точку М(х, у, z).