Приняв во внимание, что вероятность появления герба при бросании монеты равна 0,5, убеждает, что относительная частота колеблется около вероятности.
4. Геометрическое определение вероятности
 Если число исходов испытания
бесконечно, то иногда удобно пользоваться геометрическим определением
вероятности Р(А). Схема использования этого определения состоит в следующем.
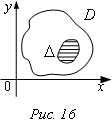
Пусть в область D наудачу
бросается материальная точка. Найти вероятность попадания точки в область D.
Если число исходов испытания
бесконечно, то иногда удобно пользоваться геометрическим определением
вероятности Р(А). Схема использования этого определения состоит в следующем.
Пусть в область D наудачу
бросается материальная точка. Найти вероятность попадания точки в область D.
Вероятность попадания точки в область D пропорциональна площади D и не зависит от расположения D в D.
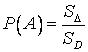 .
.
Если рассматривать одномерные объекты, то речь идет о длине областей D, D; для двумерных – о площади областей D, D (как в примере); для трехмерных – об объеме областей. Единое название длины, площади, объема – мера области.
Тогда
 .
.
Пример Задача о встрече.
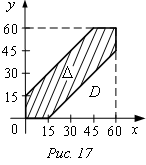 Два
студента условились встретиться в определенном месте между 14 и 15 часами.
Пришедший первым ждет другого 15 минут, после чего уходит. Чему равна
вероятность встречи студентов, если приход каждого из них в течение указанного
часа может произойти в любое время?
Два
студента условились встретиться в определенном месте между 14 и 15 часами.
Пришедший первым ждет другого 15 минут, после чего уходит. Чему равна
вероятность встречи студентов, если приход каждого из них в течение указанного
часа может произойти в любое время?
Пусть х – время прихода первого студента,
у – время прихода второго студента.
Студенты
встретятся, если между их приходами разница будет не более 15 мин., т.е. ![]() или
или ![]() .
.
Граничные линии этих областей
– прямые ![]() и
и
![]() .
.
А: встреча состоится. 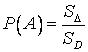 ;
;
![]() ;
;
![]()
![]() .
.
5. Элементы комбинаторики
Пусть имеем множество n однородных элементов. Комбинаторика изучает возможности составления и подсчета количества комбинаций, которые можно составить из элементов исходной группы, и подчиняющихся определенным условиям. Комбинации элементов по-другому называются соединениями.
1)
Пусть все элементы исходной группы участвуют в создании комбинаций, ![]() , где m– количество элементов в комбинации.
, где m– количество элементов в комбинации.
Пример Найти количество
последовательностей номеров из цифр ![]() .
.
Получим
следующие комбинации: ![]() . (6 шт.)
. (6 шт.)
Комбинации
отличаются одна от другой только порядком следования элементов. Такие
комбинации называются ПЕРЕСТАНОВКИ, обозначаются Рn
и количество всех перестановок из n
элементов равно ![]() ;
; ![]() .
.
В
примере n = 3; ![]() .
.
2)
Пусть не все элементы исходной группы участвуют в создании комбинаций, ![]() .
.
Пример 1 Составить все возможные отношения из трех чисел а, в, с по два числа (без повтора элементов).
Получим
следующие комбинации: ![]() . Их 6 шт. и они
отличаются одна от другой или элементами, или порядком их следования, или тем и
другим. Такие комбинации называются РАЗМЕЩЕНИЯ, обозначаются
. Их 6 шт. и они
отличаются одна от другой или элементами, или порядком их следования, или тем и
другим. Такие комбинации называются РАЗМЕЩЕНИЯ, обозначаются ![]() и количество всех размещений из n
элементов по m равно
и количество всех размещений из n
элементов по m равно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.