Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 32

;  .

Определение  Центральным моментом порядка k случайной величины Х называется .

Для ДСВ Х   , для НСВ Х .

Центральный момент первого порядка μ₁ = 0. Действительно, .

Если распределение симметричное, то все нечетные центральные и начальные моменты равны нулю.

Начальные и центральные моменты связаны между собой: ;  ;  и т.д.

Нормальное распределение на практике редко встречается в идеальном виде. Чтобы оценить отклонение экспериментальной плотности вероятности от идеальной f(x) с одними и теми же параметрами а и σ, пользуются асимметрией А и эксцессом Е:  ;  .

Если , то и «левое плечо» к экспериментальной кривой распределения пологое; Если , то «правое плечо» пологое.

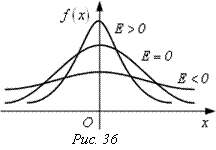
Эксцесс Е используется для характеристики крутости кривой распределения.

Для нормального закона распределения

А = 0;  Е = 0,  т.е.  .

в) Показательный закон распределения

Определение  Показательным (экспоненциальным) распределением случайной величины Х называется такое распределение, которое описывается дифференциальной функцией распределения вида

Рис. 32

Рис. 32

.

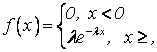
     – параметр распределения.

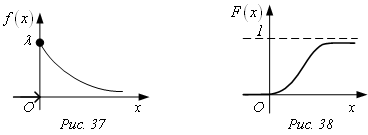
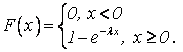
Графики f(x) и F(x):

.

;  .

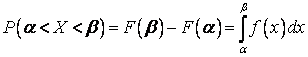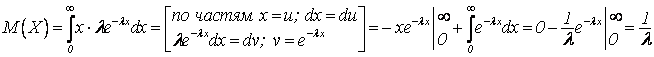
Итак, для показательного закона распределения .

Показательный закон распределения встречается в теории надежности, в теории массового обслуживания, в автоматизации (функция надежности и время безотказной работы элемента) и т.д.

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА (МС)

1. Основные понятия

Предмет МС – любой объект, изучаемый с количественной стороны в целях более точной оценки его качественного состояния.

При этом имеются в виду групповые объекты, т.е. явления массовые, в сфере которых проявляют свое действие статистические законы.

Единица наблюдения – составной элемент или член группового объекта.