Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 16

Замечание 1) если (n – q) – нецелое, то (nр + р)– тоже нецелое, т.к. р+ q = 1. Тогда между этими числами есть единственное целое положительное число т.

2) Если (n – q) – целое, то и (nр + р) – целое, тогда т имеет два последовательных целых значения.

Пример  Всхожесть семян составляет в среднем 80%. Найти наивероятнейшее число всхожих семян среди 9 шт.

n = 9;  р = 0,8;  q = 0,2;  ;

;  .

Следовательно, т = 7  или т = 8.

;

.

3. Локальная теорема Лапласа

При большом числе испытаний n вычисление Р_n(k) затруднительно.

Определение  Функция j(х) называется асимптотическим приближением функции f(х), если  .

Локальная теорема Лапласа

,  при , , .

Т.е. при достаточно больших n можно пользоваться приближенной формулой:

.

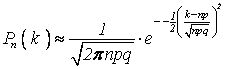Функция называется дифференциальной функцией Лапласа, табулирована на [0; 5].

Свойства j(х):

1.  j(х) определена для любых х;

2.  имеет один максимум в т. А(0; 0,39);

3.  имеет две точки перегиба при х =  ± 1;

4.  имеет одну горизонтальную асимптоту ; ;

5.   j(х) четная;;  ; симметричная относительно оси ОУ;

6.  при х = 5  j(х) = 0,0000015, т.е. практически при  .

Итак, локальная формула Лапласа  .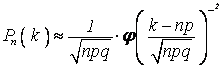

Пример  Монета брошена 100 раз. Найти вероятность того, что герб появится 32 раза.

n = 100, k = 32, А: появление герба; ; .

.

4. Формула Пуассона

Если n велико, а вероятность р достаточно мала, то локальная теорема Лапласа недостаточно точна. В этих случаях используют формулу Пуассона.

Теорема  Если вероятность появления события А в каждом испытании мала , число независимых испытаний достаточно велико , но  остается небольшим, то вероятность наступления события А ровно k раз в n независимых испытаниях равна

,   λ = n р.

Формула табулирована для разных λ и k.