Пример Вероятность изготовления нестандартной детали р = 0,004. Найти вероятность того, что среди 1000 деталей 5 нестандартные.
n = 1000, k = 5; р = 0,004; λ = nр = 4.
![]() .
.
Если
считать этот вариант по формуле Бернулли, получим ![]() ;
по локальной формуле Лапласа имеем
;
по локальной формуле Лапласа имеем ![]() .
.
5. Интегральная теорема Лапласа
Теорема Если вероятность
р наступления события А постоянна в каждом из n независимых
испытаний, ![]() , то вероятность
, то вероятность ![]() того, что событие А появится
в n испытаниях от k1 до k2 раз приближенно равна определенному интегралу
того, что событие А появится
в n испытаниях от k1 до k2 раз приближенно равна определенному интегралу
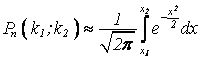 , где
, где 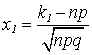 ;
;
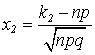 .
.
Функция
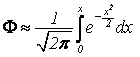 называется интегральной функцией
Лапласа или интегралом вероятности, табулирована.
называется интегральной функцией
Лапласа или интегралом вероятности, табулирована.
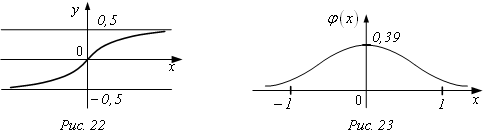
Свойства F(х):
1. F(х) определена для любого х.
2. F(х) не имеет экстремумов.
3. F(х) имеет одну точку перегиба О(0,0).
4.
Имеет две горизонтальные асимптоты![]() .
.
5. F(х) нечетная, F(-х) = - F(х); симметричная относительно О(0,0).
6. Пересекает оси в т. О(0,0).
7.
При х = 5 F(х) = 0,
49999997, т.е. практически при ![]() F(х) = 0,5.
F(х) = 0,5.
8. F(х) есть первообразная для j(х).
Итак:
![]() , где
, где 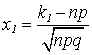 ;
;
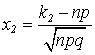 . Формула называется интегральной
формулой Лапласа.
. Формула называется интегральной
формулой Лапласа.
Пример Монету бросают
100 раз. Найти вероятность того, что герб выпадет от 32 до 60 раз. n
= 100, k1 = 32, k2 = 60; А: выпадение герба; ![]() ;
;
![]() .
.

![]() .
.
6. Вероятность отклонения относительной частоты события А от его теоретической вероятности
Пусть
проведено n независимых испытаний, в т из них событие А
появилось. Относительная частота появления события ![]() .
Теоретическая вероятность появления события Ав каждом из n
независимых испытаний равна р.
.
Теоретическая вероятность появления события Ав каждом из n
независимых испытаний равна р.
![]()
![]() Требуется
найти
Требуется
найти ![]() , где e – заданное число. Событие
, где e – заданное число. Событие ![]() запишем
по-другому:
запишем
по-другому: ![]() или
или ![]() .
Отсюда
.
Отсюда ![]() . Используя интегральную формулу Лапласа,
найдем требуемую вероятность:
. Используя интегральную формулу Лапласа,
найдем требуемую вероятность: 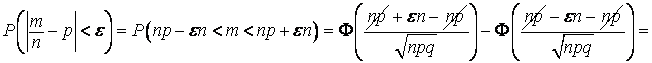
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.