Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 42

Пример(**):  x_i   9,0   9,8   10,6   11,4   12,2   13,0   13,8   14,6

                        n_i    2      6       15      23     25      17       7        5

1) .

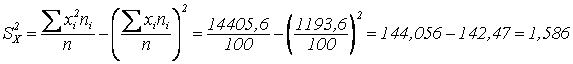2) .

3) Поправка Шеппарда:.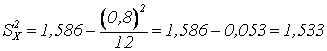

4) . В нашем примере можно не использовать поправку.

е) Коэффициент вариации

Дисперсия  и СКО  применима для сравнительной оценки одноименных величин. На практике довольно часто приходится сравнивать изменчивость признаков, выраженных разными единицами. В этих случаях используют не абсолютные, а относительные показатели вариации.

Коэффициент вариации С_V есть среднее квадратическое отклонение, выраженное в процентах от величины средней арифметической:

.

Пример  Сравнить два варьирующих признака. Среднее  и СКО  для первого признака. Для второго , . Следует ли отсюда, что Х₂ варьирует сильнее, чем Х₁?

;  .

Следовательно, сильнее варьирует признак Х₁.

Отметим, варьирование признака Х слабое, если С_V < 10%; среднее, если 10% < С_V <25%; значительное, если С_V >25%.

4.3 Структурные средние

На величину средней арифметической  могут значительно влиять крайние члены ранжированного вариационного ряда, которые как раз и наименее характерны для данной совокупности. Структурные средние представляют собой конкретные варианты имеющейся совокупности, которые занимают особое место в ряду распределения.

а) Медиана Ме – средняя, которая делит ряд распределения на две равные части. По обе стороны от медианы располагается одинаковое число вариант.

Если число вариант небольшое, то данные ранжируют и при нечетном n центральная варианта и есть медиана.

Пример    x_i:   12   14   16   18   20   22   24   26   28 ,    n = 9

Ме(Х) = 20.

Если число вариант четное, то медиана равна полусумме его центральных членов.

Пример    x_i:   6   8   10   12   14   16   18   20   22   24 ,    n = 10

Если ряд вариационный интервальный, то  .

Вначале находят класс, к которому принадлежит медиана Ме(Х). Для этого частоты n_i ряда кумулируют (накапливают) в направлении от меньших к большим значениям классов до величины, превосходящей половину всех членов данной совокупности, т.е. . Первая величина в ряду накопленных частот, которая больше , соответствует медианному классу; частота этого класса n_Ме; нижняя граница Ме – класса обозначается х_н;  – величина классового интервала; Sn_i – накопленная частота класса, предшествующего Ме – классу.