 |
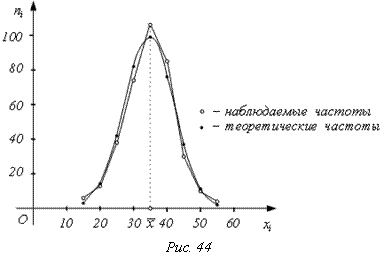
Обычно ni и ![]() различаются. Возможно, что
расхождение случайно и связано с ограниченным числом наблюдений; возможно, что
расхождение неслучайно (значимо) и объясняется тем, что для вычисления
выравнивающих частот была выдвинута статистическая гипотеза о том, что
генеральная совокупность распределена нормально, а в действительности это не
так. Распределение генеральной совокупности, которое она имеет в силу
выдвинутой гипотезы, назовем теоретическим. В примере теоретическое
распределение – нормальное; наблюдаемое распределение – эмпирическое.
различаются. Возможно, что
расхождение случайно и связано с ограниченным числом наблюдений; возможно, что
расхождение неслучайно (значимо) и объясняется тем, что для вычисления
выравнивающих частот была выдвинута статистическая гипотеза о том, что
генеральная совокупность распределена нормально, а в действительности это не
так. Распределение генеральной совокупности, которое она имеет в силу
выдвинутой гипотезы, назовем теоретическим. В примере теоретическое
распределение – нормальное; наблюдаемое распределение – эмпирическое.
Возникает необходимость установить критерий
(правило), который позволит судить, является ли расхождение между ni и ![]() случайным или
значимым.
случайным или
значимым.
если расхождение случайно, то говорим, что данные выборки согласуются с гипотезой о распределении генеральной совокупности и, следовательно, гипотезу можно принять. Если же расхождение значительно, то гипотезу следует отвергнуть.
Критерий согласия – критерий, который позволяет судить о том, что расхождения эмпирического и теоретического распределения случайно или значимо (принимать гипотезу или отвергать).
Обозначим через ![]() величину
величину
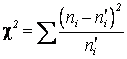 .
.
Чем больше согласуются эмпирическое и теоретическое
распределения, тем меньше ![]() . Величина
. Величина ![]() – случайная, ее дифференциальная
функция распределения зависит только от числа k степенной
свободы.
– случайная, ее дифференциальная
функция распределения зависит только от числа k степенной
свободы.
При проверке гипотезы о нормальном распределении k = S – 3, где S -
число групп, на которые разбиты данные наблюдений. Далее, при выбранном уровне
значимости α (или доверительной вероятности γ = 1 – α) по таблице приложения найдем
![]() .Если расхождение случайно, то
.Если расхождение случайно, то ![]() (гипотеза принимается). Если
расхождение значимо, то
(гипотеза принимается). Если
расхождение значимо, то ![]() (гипотеза
отвергается).
(гипотеза
отвергается).
В примере
![]() ;
; ![]() ;
; ![]() ;
; ![]() . Т.к.
. Т.к. ![]() , то гипотеза о нормальном
распределении генеральной совокупности не отвергается.
, то гипотеза о нормальном
распределении генеральной совокупности не отвергается.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М. : Высшая школа, 1972 - 1998, 368 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М. :Высшая школа, 1975 – 1999, 400 с.
3. Данко П.Е., Попов А.Г. и др. Высшая математика в упражнениях и задачах. т. 2 – М. : Высшая школа, 1980 – 1990, 415 с.
4. Засуха В.А., Лисенко В.П., Голуб Б.Л. Прикладная математика. – Киев, 2005, 303 с.
5. Лакие Г.Ф. Биометрия. – М. : Высшая школа, 1990, 325 с.
6. Румшиский Л.З. Математическая обработка результатов эксперимента. – М. : Наука, 1971, 192 с.
![]()
Ершова Тамара Григорьевна
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.