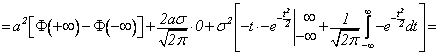
![]() .
.
![]() .
.
Тогда
![]() .
.
Примеры 1) Написать формулу плотности нормального распределения, если его параметры а = 3 и σ = 1.
2)
Найти числовые характеристики нормального распределения Х, если
плотность вероятности  .
.
3)
Является ли функция 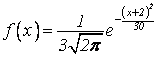 плотностью нормального распределения?
плотностью нормального распределения?
Функция
распределения F(x) для
нормальной случайной величины имеет вид:  и
неудобна для использования в задачах. Сделаем замену переменной
и
неудобна для использования в задачах. Сделаем замену переменной ![]() , т.е. нормируем величину Х,
тогда в задачах можно использовать интегральную функцию Лапласа
, т.е. нормируем величину Х,
тогда в задачах можно использовать интегральную функцию Лапласа 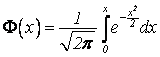 , табулированную.
, табулированную.
1. Найти вероятность попадания Х в заданный интервал

![]()
Вывод Чтобы найти ![]() , необходимо нормировать границы
, необходимо нормировать границы ![]() ,
, ![]() и найти значения Φ(х) в этих точках по
таблице.
и найти значения Φ(х) в этих точках по
таблице.
![]() .
.
2) Найти вероятность заданного отклонения
![]()
![]()
Итак:
![]() .
.
3) Правило «3-х сигм)
![]() (
(![]() значений
Х попадут в интервал (а – σ; а + σ)).
значений
Х попадут в интервал (а – σ; а + σ)).
![]() .
.
![]() .
.
Вывод: с вероятностью 0,9973 (близкой к единице) можно утверждать, что значения нормальной случайной величины находятся в интервале (а - 3σ; а + 3σ). Длина интервала 6σ.
Пример: 1) Размер деталей, изготовленных на станке-автомате, подчиняется нормальному закону, σ = 3 мм. Найти вероятность того, что размер наудачу взятой детали отклонится от проектного размера 12 см не более, чем на 5 мм (или найти количество деталей из 100 с данным допуском).
Имеем: а = 12 см; σ = 3 мм = 0,3 см; e = 0,5 см.
![]() .
.
Следовательно, около 90 шт. деталей из 100 шт. поступают с таким допуском.
2) Найти интервал, в который с вероятностью 0,9973 попадут детали со станка-автомата.
![]() ;
; ![]() ;
;
![]() .
.
Понятие о центральной предельной теореме Ляпунова:
Если случайная величина Х представляет собой сумму большого числа случайных величин Х1, Х2, ..., Хn с любыми законами распределения, то она распределена нормально, при этом важно, чтобы среди слагаемых случайных величин Хi не было резко выделяющихся по значению σi.
Понятие о моментах распределения:
Определение Начальным
моментом порядка k случайной величины Х называется ![]() .
.
Для
ДСВ Х  ; для НСВ Х
; для НСВ Х 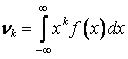 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.