Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 21

2. Числовые характеристики дискретной случайной величины Х

Определение   Числовыми характеристиками случайной величины Х называются такие характеристики, которые в сжатой форме (одним числом) выражают наиболее существенные особенности распределения.

Наиболее часто применяемые характеристики – математическое ожидание, дисперсия, среднее квадратическое отклонение, мода, медиана.

Математическое ожидание, мода и медиана называются характеристиками положения случайной величины, т.е. указывают некоторое среднее ориентировочное значение, около которого группируются все возможные значения случайной величины.

Среднее значение случайной величины есть некоторое число, являющееся как бы ее «представителем» и заменяющее ее при грубых ориентировочных расчетах: «среднее» время работы прибора, «средняя успеваемость», «средняя зарплата» и т.д.

Из характеристик положения в теории вероятностей важнейшую роль играет математическое ожидание случайной величины или среднее значение величины.

1. Математическое ожидание

Определение  Математическим ожиданием дискретной случайной величины Х, заданной законом распределения 

называется сумма парных произведений всех ее возможных значений на соответствующие вероятности:  .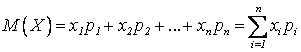

Физическая интерпретация М(Х): Пусть на оси ОХ расположены точки с координатами  х₁, х₂, ..., х_n, в которых сосредоточены соответственно массы         р_1, р_2, ..., р_n , причем 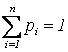. Тогда М(Х) есть не что иное, как абсцисса центра тяжести данной системы материальных точек.

Вероятностный смысл М(Х): Предположим, что в законе распределения заданы не теоретические вероятности р_i, а относительные частоты значений х_i, тогда говорят, что задано статистическое распределение:

, где n – общее количество проведенных наблюдений; n_i, - количество наблюдений, в которых величина Х приняла значение х_i;n₁ + n₂ + ...+ n_k = n. Тогда