Числовые характеристики распределения:
 ;
; 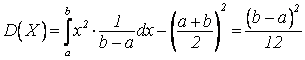 ;
;
![]() ;
;
![]() ; величина Х моды не имеет. Вероятность
попадания равномерно распределенной величины Х в заданный интервал
; величина Х моды не имеет. Вероятность
попадания равномерно распределенной величины Х в заданный интервал 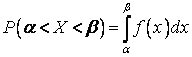 .
.
б) Нормальный закон распределения – самый распространенный в нашем мире.
Определение Случайная
величина Х распределена нормально, если ее плотность вероятностей 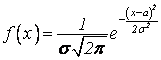 , при этом числа а и s называются параметрами нормального распределения, коротко N(a;s). График
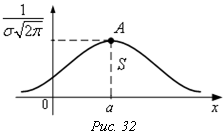
дифференциальной функции нормального распределения называют нормальной
кривой или кривой Гаусса.
, при этом числа а и s называются параметрами нормального распределения, коротко N(a;s). График
дифференциальной функции нормального распределения называют нормальной
кривой или кривой Гаусса.
Исследуем
f(x): 1) о.о.ф.
![]() ;
;
 2) имеет один экстремум – тах
в
2) имеет один экстремум – тах
в 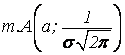 ;
;
3) имеет две точки перегиба при х= а - s , х = а + s;
4) симметрична относительно прямой Х = а
5) имеет горизонтальную асимптоту у = 0,
![]() ;
;
![]() .
.
6) ![]() .
.
Если
для случайной величины Х, нормально распределенной, параметры распределения а
= 0, s = 1, то 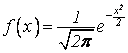 – это дифференциальная функция j(Х) Лапласа,
табулированная, используемая ранее в локальной теореме Лапласа.
– это дифференциальная функция j(Х) Лапласа,
табулированная, используемая ранее в локальной теореме Лапласа.
Определение Нормальная случайная величина Х с параметрами а = 0, s =1, (N(0;1)) называется нормированной нормальной случайной величиной.
Следовательно, дифференциальная функция Лапласа j(Х) есть плотность нормированного нормального распределения.
Определение Нормированием
случайной величины Х называется линейная операция ![]() ;
; ![]() ;
;
![]() .
.
Если в формуле f(x) изменяется параметр а, то кривая f(x), не изменяя формы, перемещается вдоль оси ОХ в точку симметрии х = а.
Если изменяется параметр s, то кривая j(Х) либо уплощается при увеличении s, либо становится более островерхой при уменьшении s.
Найдем числовые характеристики нормально распределенной величины Х

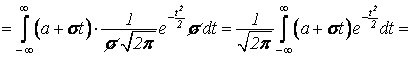
![]()
![]()
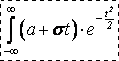
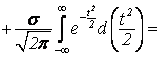
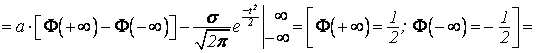
![]() .
.
Следовательно, М(Х)=а.
Аналогично,
можно показать, что ![]() . Известно, что
. Известно, что ![]() . Найдем
. Найдем 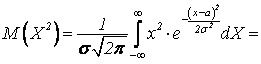
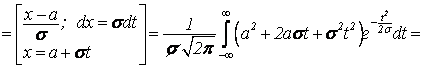
![]()
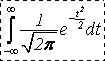
![]()

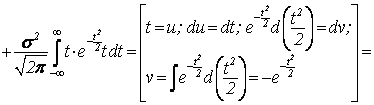
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.