Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 25

Пример  Пусть случайная величина Х задана законом распределения:

. Найти числовые характеристики М(Х), D(X), s(Х).

1)

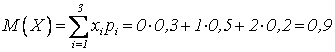
2)

3) ;  .

Свойства дисперсии

1) D(C) = 0;  С = const.

2) .

3) , если Х, У – независимые случайные величины.

4) .

5) Пусть Х биномиально распределенная величина, число появлений события А в n независимых испытаниях, р(А) = р в каждом испытании.

Пусть Х₁ – число наступления события А в первом испытании; Х₂ – во втором и т.д.; Х_n – в n-ом испытании. Тогда Х = Х₁ + Х₂ +...+ Х_n, причем величины Х_i взаимно независимы, т.к. исход каждого испытания не зависит от исходов других испытаний. Поэтому D(X) = D(X₁) + D(Х₂) + ...+ D(Х_n).

; ;

. Тогда D(X) = D(X₁) + D(Х₂) + ...+ D(Х_n) = nрq.

Итак: для биномиально распределенной величины Х   .

6) Пусть Х – случайная величина, распределенная по закону Пуассона, , λ – параметр закона.

3. Среднее квадратическое отклонение (СКО) суммы взаимно независимых случайных величин

Теорема  СКО суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов СКО этих величин

Пусть Х = Х₁, Х₂, ..., Х_n;

D(X) = D(X₁) + D(Х₂) + ...+ D(Х_n);

;

.

4. Одинаково распределенные взаимно независимые случайные величины

Известно, что по закону распределения можно найти его числовые характеристики, следовательно, если несколько случайных величин имеют одинаковое распределение, то их числовые характеристики одинаковы.

Пусть случайные величины Х₁, Х₂, ..., Х_n имеют одинаковое распределение. Обозначим  – среднее арифметическое случайных величин и М(Х_i) = а;  D(X_i) = D,  i = 1, 2,   , n.