Определение Доверительной вероятностью называется вероятность
![]()
На практике γ: 0,9; 0,95; 0,99; 0,9999, в зависимости от объекта и целей исследования (вероятность практически достоверного события).
Противоположная
вероятность α = 1 – γ называется уровнем значимости (вероятность практически
невозможного события), α: 0,1; 0,05; 0,001; 0,0001. Интервал ![]() или
или ![]() называется
доверительным, нижняя граница U* - δ, верхняя
граница U* + δ.
называется
доверительным, нижняя граница U* - δ, верхняя
граница U* + δ.
Говорим, что доверительный интервал заключает в себе Uг с вероятностью (надежностью) γ.
Для любой выборочной характеристики по соответствующей методике можно найти доверительный интервал с надежностью γ.
Например,
пусть количественный признак Х распределен нормально, причем МГ = а
неизвестно, а СКО σГ = σ. Найдем доверительный интервал параметра а
(по-другому, а есть истинное значение случайного признака Х). Будем оценивать
неизвестное математическое ожидание признака Х по выборочной средней ![]() .
.
![]() с одной стороны. С другой стороны
с одной стороны. С другой стороны 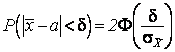 . Для
. Для ![]() СКО
СКО
![]() . Тогда
. Тогда 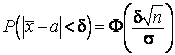 ;
;
![]() и
и ![]() –
точность оценки.
–
точность оценки.
Следовательно,
![]() .
.
Итак,
имеем ![]() и
и ![]() .
.
Отсюда
![]() ;
; ![]() и
t можно найти по таблице функции Ф(х).
и
t можно найти по таблице функции Ф(х).
Таким
образом, интервал ![]() будет доверительным для параметра
а с надежностью γ.
будет доверительным для параметра
а с надежностью γ.
Пример Количественный
признак Х распределен нормально и σ = 3. Найти доверительный интервал для
параметра а с надежностью γ = 0,95, если проведено n =
36 наблюдений и ![]() = 4,1.
= 4,1.
2Ф(t) = 0,95; Ф(t) = 0,475; t = 1,96.
Точность
оценки ![]() .
.
Доверительный интервал: 4,1 – 0,98 < a <4,1 + 0,98 или 3,12< a < 4,08.
Надежность γ = 0,95 указывает, что, если будет произведено большое количество k выборок, то в 95% из них параметр а действительно заключен в этих границах; в 5% этих выборок параметр а может выйти за эти границы, т.е. доверительная вероятность γ не связана с оцениваемым параметром, она связана с границами доверительного интервала, которые изменяются от выборки к выборке.
Рассмотрим случай, когда СКО σГ = σ неизвестно и признак Х распределен нормально. Задача была решена английским статистиком В. Госсетом (псевдоним Стьюдент).
Случайная
величина 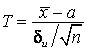 имеет закон распределения, не
зависящий от а и σ, зависящий только от n,
называется t-распределение или распределение Стьюдента.
Дифференциальная функция этого распределения (плотность вероятности) – S(t; n). Тогда
имеет закон распределения, не
зависящий от а и σ, зависящий только от n,
называется t-распределение или распределение Стьюдента.
Дифференциальная функция этого распределения (плотность вероятности) – S(t; n). Тогда
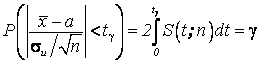 .
.
Доверительный
интервал: 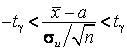 или
или 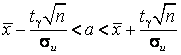 ,
величина tγ табулирована при любых γ и n.
,
величина tγ табулирована при любых γ и n.
Пример Количественный
признак Х генеральной совокупности распределен нормально. По выборке объемом n =
16 найдены ![]() и
и ![]() .
Оценить неизвестное значение а признака Х с помощью доверительного
интервала при надежности γ = 0,95.
.
Оценить неизвестное значение а признака Х с помощью доверительного
интервала при надежности γ = 0,95.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.