Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 14

: формулы нет ни в одном справочнике.

. Тогда .

5. Формула полной вероятности (ФПВ)

Пример  В магазин поступают лампочки с двух заводов, с завода №1 – 70%, с завода №2 – 30%. Из каждый 100 шт. на заводе №1 90 стандартные; на заводе №2 из 100 шт. 80 стандартные.

Наудачу купили одну лампочку. Какова вероятность, что она стандартная?

Пусть А: лампочка стандартная. Относительно купленной лампочки может возникнуть два предположения (гипотезы): В₁ – лампочка изготовлена на заводе №1; В₂ – лампочка с завода №2.

Событие А в этом случае можно представить в виде (лампочка стандартна, если она с завода №1 и стандартна или с завода №2 и стандартна).

События  АВ₁ зависимые и события АВ₂ тоже зависимые.

События и  несовместные. Тогда, используя теоремы умножения и сложения, имеем

По условию задачи Р(В₁) = 0,7; Р(В₂) = 0,3; ; .

Следовательно, .

Обобщение  Если интересующее нас событие А может произойти только в результате осуществления одного из несовместных событий В₁, В₂, ..., В_n, составляющих ПГНС, то вероятность события А равна сумме парных произведений вероятностей событий В₁, В₂, ..., В_n, называемых гипотезами или предположениями, на соответствующие условные вероятности события А:

.

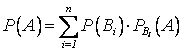6. Формула Байеса (формула пересчета вероятности гипотез)

Пусть событие А может произойти в результате осуществления одной из гипотез В₁, В₂, ..., В_n, составляющих ПГНС. Пусть событие А произошло. Пересчитаем вероятность i-той гипотезы в этом случае, т.е. найдем Р_А(В_i).

По теореме умножения имеем:

.  Отсюда 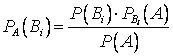 , в этом случае Р(А) – есть полная вероятность события А.

Формула 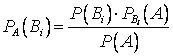 называется формулой Байеса.

Пример:  Возьмем условие предыдущего примера.

Пусть купленная наудачу лампочка оказалась стандартной. Найти вероятность того, что лампочка изготовлена на заводе №1, т.е. требуется пересчитать вероятность гипотезы В₁.

.

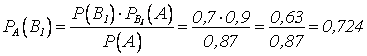8. Схема испытаний Бернулли (повторение независимых испытаний)

1. Формула Бернулли

Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.

В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем рассматривать второй случай.

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться с одной и той же вероятностью р, .