Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 18

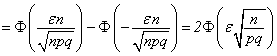
Итак: .

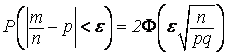Пример:  Вероятность того, что деталь нестандартна р = 0,1. Найти, сколько деталей надо отобрать, чтобы с вероятностью р = 0,9544 можно было утверждать, что относительная частота появления нестандартных деталей среди отобранных отклонится от постоянной вероятности р по абсолютной величине, не более чем на 0,03.

р = 0,1;  e = 0,03;  Р = 0,9544;  . n - ?  q = 0,9.

.

;  .

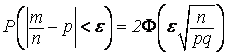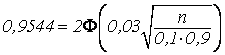По таблице Ф(х) имеем Ф(2) = 0, 4772. Следовательно ;  n = 400.

Вероятностный смысл результата: если взять достаточно большое число проб по 400 деталей, то в 95,44% этих проб относительная частота появления нестандартных деталей W(A) будет отличаться от постоянной вероятности р = 0,1, не более, чем на 0,03, т.е. W(A) будет заключена в границах:

 или

; 7% от 400 деталей равно 28 деталям; 13% от 400 шт. равно 52 деталям.

Тогда число нестандартных деталей в 95,44% проб будет заключено от 28 до 52 шт., т.е. .

Если взять лишь одну пробу из 400 деталей, то с вероятностью 0,9544 можно ожидать, что нестандартных деталей в ней будет не менее 28 и не более 52.

Возможно, хотя и маловероятно (0,0456) для одной пробы, что нестандартных деталей будет меньше 28 или больше 52.

Вывод. Закон больших чисел в форме Бернулли

Если производится n независимых испытаний, в каждом из которых событие А появляется с одной и той же вероятностью, близкой к единице, т.е. почти достоверно, можно утверждать, что относительная частота события W(A) будет сколь угодно мало (e) отличаться от вероятности этого события в одном испытании: , т.к. .

Эта теорема имеет фундаментальное значение для приложений теории вероятностей к статистике, т.к. позволяет вместо вероятности использовать относительную частоту события.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

1. Основные понятия

Определение  Случайной величиной называется величина, которая в результате опыта может принять то или иное значение из своих возможных значений, заранее неизвестно – какое именно.

Различаем случайные величины прерывного (дискретного) и непрерывного типа. Обозначаем случайные величины X, Y, Z их значения x_i, y_j, z_k.

Определение  Случайная величина Х называется дискретной, если она принимает отдельные изолированные значения с определенной вероятностью. Число возможных значений Х может быть конечно или бесконечно, но в этом случае их можно перенумеровать или пересчитать. Такое множество значений дискретной случайной величины Х называется счетным множеством.

Примеры:  1) число выпадений герба при пяти бросаниях монеты;

2) число отказавших элементов в приборе, состоящем из шести элементов;

3) число пробоин в мишени при четырех выстрелах и т.д.

Определение  Величина Х называется непрерывной, если ее возможные значения заполняют непрерывно некоторый интервал.

В этом случае значения Х не могут быть перечислены заранее. Такое множество значений называется континуум.