Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 23

4) , доказывается аналогично свойству 3.

5) Пусть случайная величина Х распределена по биномиальному закону (пр.2).

Тогда , где n – число независимых испытаний, р – вероятность появления события А в каждом испытании; Х – число появлений события А в n независимых испытаниях.

Пусть Х₁ – число появлений события А в первом испытании, Х₂ – во втором испытании, ..., Х_n – в n-ом испытании, общее число появлений события А во всех испытаниях равно  Х = Х₁ + Х₂ + ..., Х_n. По свойству математического ожидания имеем М(Х) = М(Х₁) + М(Х₂) + ... + М(Х_n).

Так как математическое ожидание числа появлений события А в одном испытании равно вероятности появления А (см. пр.1 «Индикатор события»), то М(Х) = р + р + р +...+ р = nр.

Пример  1) Проводим 20 независимых испытаний . Найти М(Х) числа появлений события А в 20 испытаниях..

2) Производится 4 выстрела с вероятностью попадания в цель р₁ = 0,6; р₂ = 0,4; р₃ = 0,5; р₄ = 0,7. Найти математическое ожидание общего числа попаданий.

М(Х) = М(Х₁) + М(Х₂) + М(Х₃) + М(Х₄) = 0,6 + 0,4 + 0,5 + 0,7 = 2,2

6) Пусть случайная величина Х распределена по закону Пуассона (пр. 3).

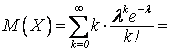[при k = 0 первый член равен нулю]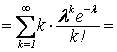

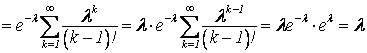. Следовательно, М(Х) = λ.

2. Меры рассеивания значений Х около центра распределения М(Х)

Пример  Пусть две бригады выполняют одну и ту же работу, в бригадах по 3 человека. Их выработка за смену:

Х:   99,  100,  101; 

Y:   90,  100,  110;  .