Математика \ Теория вероятностей и математическая статистика

Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 48

Найдем ; . (Проверка: т. должна лежать на линиях регрессий  и ).

Найдем девиаты: ;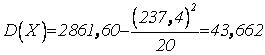

                              .

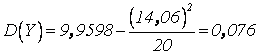Найдем коэффициент корреляции: , т.е. rxy указывает на наличие положительной корреляционной связи между Х, У средней силы. Принято считать связь слабой, если ; средней, если ; сильной, если  и значительной, почти функциональной .

Эмпирический коэффициент корреляции, как и другой выборочный показатель служит оценкой для генерального (истинного) коэффициента корреляции.

Его ошибка 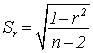 . Значимость коэффициента корреляции rxy, т.е. отличие теоретического коэффициента корреляции от нуля, можно проверить по   Н-критерию. Задаем доверительную вероятность γ и вычисляем величину . В нашем примере rxy=0,564; n=20; γ=0,95. . Найдем по таблице Нкрит при γ=0,95 и n=20. Нкрит=1,94. (Румшисский, с. 190;      с. 114-115).

Т.к. Нкрит< Ннабл. гипотезу о некоррелированности Х, Уотвергаем, т.е. теоретический коэффициент корреляции отличен от нуля или значимый.

Найдем уравнение регрессии массы тела детеныша  по значениям массы их матерей по МНК: .

;   .

;   .

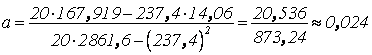Уравнение регрессии массы тела детеныша  по значениям массы тела их матерей хi оказывается следующим: .

Это означает, во-первых, что с увеличением массы тела матери на 1 кг масса тела новорожденных детенышей увеличивается в среднем на 0,024 кг.

Во-вторых, подставляя в это уравнение вместо х конкретное значение массы тела матери, можно определить вероятную (среднюю) массу новорожденного детеныша.

Если  х=12 кг, то .

          х=14 кг       .  – ожидаемая масса новорожденного детеныша (Прогноз).

Задача 2  Построение нормальной кривой по опытным данным

Один из способов построения нормальной кривой по данным наблюдений следующий:

1) находим  и Sx;

2) находим выравнивающие (теоретические) частоты по формуле , где n – сумма наблюдаемых частот (объем выборки), h – разность между двумя соседними вариантами xi+1 – xi = h, 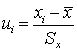;  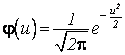 – дифференциальная функция Лапласа, табулированная.

Скачать файл