Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 40

   а)выборка не сгруппированная:

, n – объем выборки.  называется «простая арифметическая средняя»;

б) выборка сгруппирована:

, n_i – частота варианты x_i.  называется «взвешенная арифметическая средняя».

Свойства :

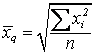б) Средняя квадратическая, :    а) ;   б) .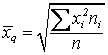

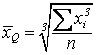в) Средняя кубическая  :    а) ;   б) .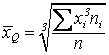

г) Средняя гармоническая

    а) 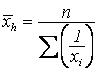;   б) .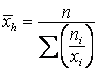

4.2 Показатели вариации

а) Лимиты: х_тin, х_тах.

б) Размах.

Пример  Х₁:   10   15   20   25   30   35   40   45   50;   .

               Х₂:    10   28   28   30   30   30   32   32   50;   .

                n = 9.

Признаки Х₁ и Х₂ имеют одинаковые лимиты и размах.

Главная черта R –не отражает существенные черты варьирования.

в) Среднее линейное отклонение

   или   .

В примере линейное отклонение признаков

d₁ :   20   15   10   5   0   5   10   15   20;   .

d₂ :   20    2     2    0   0   0    2     2    20;   .

Отсюда ;   .

Следовательно, признак Х₁ варьирует сильнее, чем Х₂.

г) Дисперсия и ее свойства

Дисперсия (или ) имеет наибольшее распространение по сравнению с другими показателями вариации. (dispersio – рассеяние, пыль; лат.)

 есть среднее арифметическое квадратов отклонений вариант от центра распределения :

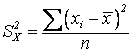   или 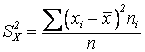   ,  при этом сумма квадратов отклонений называется девиатой:

   или   , тогда дисперсия  .

Расчетная формула дисперсии: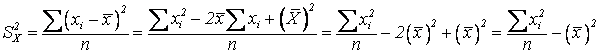

или  – среднее арифметическое квадрата величины минус квадрат среднего арифметического.

Аналог в теории вероятности дисперсия  .