Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 29

Мо(Х) = 1, т.к. Р(Х = 1) = 0,3 – наибольшая среди других вероятностей.

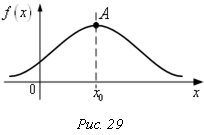
Пример 2

f(x) – плотность распределения НСВ Х т.А – точка максимума f(x), тогда х₀ = Мо(Х).

Определение  Медианой Ме(Х) случайной величины Х называется такое ее значение, которое делит площадь под кривой плотности f(x) ровно пополам, т.е. .

Для ДСВ Х медиана Ме(Х) – середина вариационного ряда значений (с учетом вероятностей р_i). Для выборки наблюдений Ме(Х) – середина упорядоченной статистической совокупности.

Мода и медиана случайной величины Х называются структурными числовыми характеристиками.

4. Законы распределения случайной величины Х

1. Для дискретной случайной величины рассмотрены два закона распределения: а) биномиальный и б) закон Пуассона.

2. Для непрерывной случайной величины рассмотрим три закона распределения.

а) Равномерный закон распределения

Определение    Равномерным распределением случайной величины Х называется такое распределение, при котором плотность распределения f(x) постоянна на интервале значений случайной величины Х, т.е. f(x) = С, если :

.

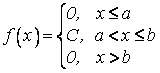Найдем значение постоянной С. Используем свойство плотности f(x):

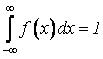. Получим . Отсюда  .

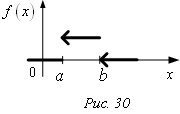Итак:

График равномерной плотности  f(x):

Функция распределения .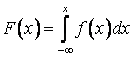

При   ;  при     ;

при   .

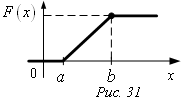
Итак .   График  F(x):

Примеры:  1) Х – ошибка округления измерения до ближайшего целого деления шкалы прибора распределены равномерно на длине целого деления.

2) Х – время прихода пассажира на остановку, если автобусы некоторого маршрута идут с достаточно малым интервалом Δt.