Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 24

Простейшей мерой рассеивания является размах , при этом х_тах, х_тin называются лимитами; R(X) = 2; R(Y) = 20. Отклонением d_i называется разность между значением и средним арифметическим  ;  . -1; 0; 1; 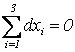 . -10; 0; 10; 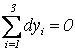 , т.е.среднее значение отклонения равно нулю.

Чтобы исключить влияние знака в качестве меры рассеивания  берут сумму модулей отклонений или сумму их квадратов.

Определение  Средним линейным отклонением называется среднее арифметическое модулей отклонений  .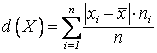

В примере ;  .

Определение  Дисперсией случайной величины Х называется среднее арифметическое квадратов отклонений 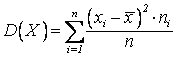 . Но размерность дисперсии не совпадает с размерностью величины Х и М(Х), поэтому в качестве меры рассеивания берут корень квадратный из дисперсии, которая называется средним квадратическим отклонением  .

В примере: ;  ;  ;  .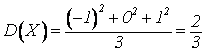

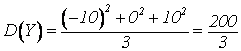Пусть случайная величина Х задана законом распределения

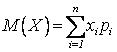;  – центр распределения величины Х

Отклонение Х есть величина случайная  .

Математическое ожидание отклонения равно нулю:   .

Дисперсия случайной величины Х равна математическому ожиданию квадрата отклонения значений Х от центра распределения М(Х): .

Физический смысл D(X):

D(X) есть аналог момента инерции системы материальных точек с весом p_i, .

Среднее квадратическое отклонение случайной величины Х обозначается

Расчетная формула дисперсии

Итак:  . Дисперсия равна разности математического ожидания квадрата величины и квадрата ее математического ожидания.