Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 41

Свойства : 1) если каждую варианту Х уменьшить или увеличить на одно и то же число А, то дисперсия не изменится.

;   .

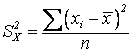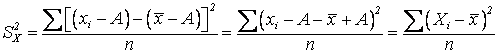Следовательно,  можно вычислять не только по x_i, но и по их отклонениям  от постоянного А.

2) Если каждую варианту Х разделить или умножить на одно и то же постоянное число А, то  уменьшится или увеличится в А² раз.

.

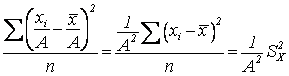Следовательно, при наличии в совокупности многозначных вариант их можно сократить на некоторое постоянное число А. Полученный после вычисления результат надо умножить на А², что и дает искомую величину дисперсии.

Свойства  и  используем в методе «условных вариант» для расчета числовых характеристик выборки. Заметим, что  называется выборочной дисперсией и является смещенной оценкой генеральной дисперсии. Чтобы получить несмещенную оценку дисперсии, которую используем в прикладных расчетах и теоретических выкладках, необходимо «исправить» выборочную дисперсию , ввести в ее формулу поправку Бесселя – множитель на «смещенность»; полученная дисперсия называется исправленной:

  или  .

При  можно использовать  и .

Пример 1) Х₁:   10   15   20   25   30   35   40   45   50;   .

     Девиата  

Дисперсия выборочная

Дисперсия исправленная

2) Х₂:   10   28   28   30   30   30   32   32   50

Девиата  .

Дисперсия выборочная ,

Дисперсия исправленная .

д) Среднее квадратическое отклонение (СКО) более удобная характеристика, чем дисперсия, т.к. выражается в тех же единицах, что Х и . Среднее квадратическое отклонение равно корню квадратному из дисперсии. Существует СКО выборочное  и СКО исправленное .

В примере  ;  .

                    ;  .

При одинаковых лимитах и размахе дисперсия и СКО не одинаковы. На их величине сказался различный характер варьирования признака.

Замечание Поправка Шеппарда

При создании безынтервального вариационного ряда из интервальной частоты n_iотносят к средним значениям классовых интервалов (см. пример**) без учета внутриклассового разнообразия. Но варианты внутри классов распределяются неравномерно, накапливаясь больше у тех границ, которые ближе к . Следовательно, при вычислении обобщающих характеристик для непрерывно варьирующих признаков допускают систематическую погрешность. Чем шире классовый интервал, тем больше эта погрешность. Учитывая это, в 1898 г. В. Шеппард установил, что разность между фактической и расчетной величиной дисперсии составляет , где λ – ширина классового интервала, т.е. поправка Шеппарда должна вычитаться из величины . Обычно поправку применяют при высокой точности расчетов или при большом числе наблюдений (), при     n < 500 поправка не используется.