Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 19

Примеры:  1) расстояние от точки попадания до центра мишени;

2) ошибка измерителя высоты;

3) время безотказной работы лампы и т.д.

Рассмотрим дискретную случайную величину Х с возможными значениями х₁, х₂, ..., х_n. Каждое из этих значений возможно, но не достоверно, и величина Х может принять каждое из них с некоторой вероятностью. В результате опыта Х примет одно из этих значений, т.е. произойдет одно из ПГНС: Х = х₁; Х = х₂; ..., Х = х_n. Тогда сумма вероятностей этих событий 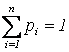. Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет описана полностью с вероятностной точки зрения, если в точности укажем, какой вероятностью обладает каждое из значений.

Определение   Законом распределения случайной величины Х называется любое соотношение, устанавливающее связь между ее возможными значениями и соответствующими вероятностями.

Про случайную величину Х в этом случае говорят, что она подчинена данному закону распределения. Если множество значений случайной величины Х конечно, то закон распределения можно задать таблицей, в которой значения х_i располагаются по возрастанию и соответствующие вероятности в сумме дают единицу:

Если множество значений бесконечно, то закон распределения задается формулой.

Примеры:  1) Каждому случайному событию А с вероятностью появления р можно поставить в соответствие случайную величину Х, которая принимает значение Х = 0, если событие А не произошло, и значение Х = 1, если событие А произошло.

                 Х в этом случае называется индикатором

        события А.