Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 5

3) z = 6 – 2х – 3у – плоскость; функция z не имеет экстремумов.

Необходимые условия экстремума 

Для функции одного переменного  необходимые условия существования экстремума: а) или б) не существует.

Аналогично можно записать необходимые условия экстремума для функции двух переменных  по каждому аргументу: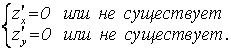

Система уравнений определяет критические или стационарные точки.

Достаточные условия определяют наличие экстремума и его тип ().

Производная по направлению вектора и градиент функции

Рассмотрим функцию  в области ее определения D. Пусть    т.М(х, у) Î D. Пусть задан вектор . Его орт 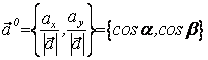, где  – направляющие косинусы вектора .

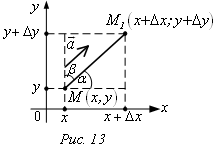На плоскости в направлении вектора  выберем т.. Аргументы х и у получили одновременно приращения Δх, Δу, тогда функция  получит соответствующее приращение, которое называется полным приращением z в данном направлении  и обозначается . Обозначим .

Определение Производной функции z в данном направлении  называется , если этот предел существует.

Полное приращение функции z имеет вид: ,  ;  ;

. Тогда

.

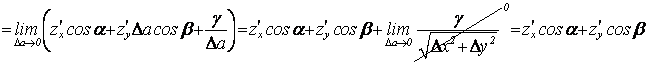Итак  – скорость изменения функции  в направлении вектора .

Определение  Градиентом  функции в т. М(х, у) называется вектор, имеющий начало в т. М и координаты , т.е.

С учетом определения , производная функции z по направлению  равна скалярному произведению  на , т.е.  .

Наибольшая скорость изменения функции z будет, если угол j между векторами равен нулю. .

Следовательно, вектор градиента указывает направление наибыстрейшего изменения функции z.