Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 15

Требуется найти вероятность того, что при n испытаниях событие А появится ровно к раз и, следовательно, не появится (n – к) раз, т.е. найти Р_n(к).

Вероятность одного сложного события, состоящего в том, что в n испытаниях А появится к раз и не появится (n-к) раз, по теореме умножения вероятностей независимых событий равна . Таких сложных событий может быть столько, сколько можно составить сочетаний . Тогда  или 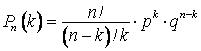. Полученная формула называется формулой Бернулли.

Пример:  1) Проводится 3 испытания Р(А) = р; . Найти вероятность того, что А появится ровно два раза.

Комбинаций 3 шт. Вероятность каждой комбинации р²q.

По теореме сложения несовместных событий имеем:

2) Монету бросаем 5 раз. Найти вероятность того, что герб выпадет 3 раза.  n = 5;  k = 3;  A: выпадение герба; ;  

2. Наивероятнейшее число наступлений события А в n независимых

 испытаниях

Определение  Число т наступлений события А в n независимых испытаниях называется наивероятнейшим, если , k = 0, 1, 2, ..., n.

Из определения следует, что ;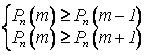

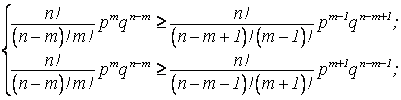
т.к. р>0,q>0,n-m>0,m>0 то, сокращая, получим:    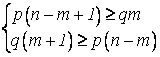 ; ; 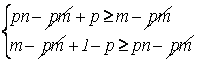 ;  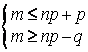  или  .