Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 22

называется средним арифметическим значением величины Х. Вычисленное значение  по данной формуле, называется средневзвешенным, т.к., частоты n_i называются весом значений х_i.

Следовательно, математическое ожидание величины Х есть среднее ожидаемое значение этой случайной величины или центр распределения случайной величины Х.

Пример  Монету бросают 3 раза. Составить закон распределения случайной величины Х – числа выпадений герба. Найти М(Х).

А: выпадение герба при одном бросании монеты; ; .

хi	0	1	2	3
рi	1/8	3/8	3/8	1/8

Закон распределения:

;

;   ;   .

.

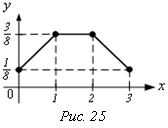
Многоугольник распределения величины Х

(рис. 25).

Определение Случайные величины Х и У называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения принимает другая случайная величина.

Пусть Х₁, Х₂, ..., Х_n – взаимно независимые случайные величины.

Свойства М(Х)

1) М(С) = С; 

2) М(СХ) = СМ(Х).

3) М(Х+У) = М(Х) + М(У);  Х, У – независимые случайные величины.

хi	х1	х2	,
рi	р1	р2

Пусть Х имеет закон распределения  

yj	y1	y2	.
Qj	Q1	Q2

У имеет закон распределения

Тогда величина Х + У будет иметь закон распределения