Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 3

Примеры  1) т.M₀ (2; 2);  .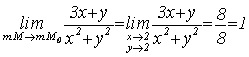

2) 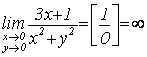;  3) .

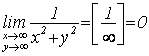ОпределениеФункция  называется непрерывной в т., если она определена в т. и .

Функция  непрерывная в каждой точке области D, называется непрерывной в этой области.

Точки, в которых не выполняется определение непрерывности  называются точками разрыва функции.

Функция может иметь отдельные точки разрыва, линии разрыва, а функция трех и более переменных может иметь поверхность разрыва.

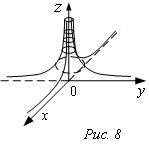
Примеры  1) ; область определения  . В т.О(0;0) z имеет разрыв (рис. 8).

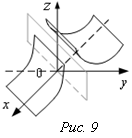
2) . Область определения . Граничная линия области D – биссектриса в плоскости ХОУ . Это линия разрыва z (рис. 9).

Определение  Частной производной  или  функции  по аргументу х называется предел отношения частного приращения  функции z по аргументу х к приращению , если последнее стремится к нулю и этот предел существует  .  Аналогично определяем  .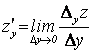

Правило отыскания : вычисляется в предположении, что аргумент х изменяется, а аргумент у не изменяется, т.е.  при дифференцировании;

 вычисляется в предположении, что , а у изменяется при дифференцировании.

Тогда при  у = С   будет функцией одного аргумента х;             при  х = С,   будет функцией одного аргумента у. Следовательно, при отыскании  используем правила дифференцирования и таблицу производных функции одного аргумента.

Примеры : 1) ;  2) ; 3) ; 4) ; 5) ;  6) .

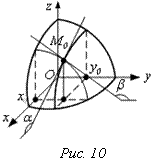Геометрический смысл

 – тангенс угла наклона α к оси ОХ, касательной к линии пересечения поверхности  и плоскости  у = у₀ ;