Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 28

, т.е. f(x) есть плотность вероятности в т.Х, т.к. величина   характеризует количество вероятности, приходящееся на единицу длины интервала Δх.

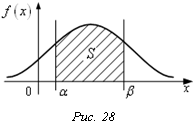Для НСВ Х можно вести речь только о вероятности принятия нею значений на некотором интервале:  .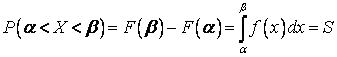

Для НСВ Х  F(x) непрерывна и вероятность того, что Х примет конкретное значение х₀, равна 0, т.е. .

Действительно, . Если , то  в силу непрерывности F(x).

Тогда  .

Следовательно, .

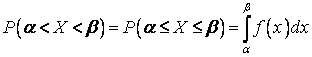Если Х принимает значения только на [a; b], то F(x) = 0  для всех   и    для всех .

Функция f(x) называется дифференциальной функцией распределения, график f(x) называется кривой распределения. Для ДСВ Х аналогом дифференциальной функции распределения является закон распределения в виде таблицы.

Свойства f(x)

1) , как производная неубывающей функции.

Вероятностный смысл f(x) – плотность вероятности, которая не может быть отрицательной.

2) .

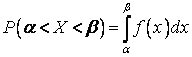3) , т.к. событие   – достоверное.

4)   для малых Δх.

,  т.е.   – вероятность того, что НСВ Х примет значения из бесконечно малого интервала dx;  f(x)dx  называется элементом вероятности.

Аналогично числовым характеристикам ДСВ Х для непрерывной случайной величины можно определить М(Х), D(X), s(Х), моду М₀ и медиану Ме. Для ДСВ Х М, D, s определяются дискретными суммами: 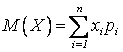 ; ; 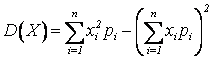 . Заменяя дискретное суммирование непрерывным суммированием или интегрированием, р_i – элементом вероятности f(x)dx , получим формулы вычисления данных числовых характеристик:

;  ;  .

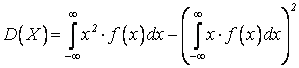Кроме М, D, s часто используют моду Мо(Х) и медиану Ме(Х).

Определение  Модой Мо(Х) случайной величины Х называется наиболее вероятное ее значение (наиболее часто встречающееся значение – «модное» значение). Мода для ДСВ Х есть наивероятнейшее число т₀; для НСВ Х Мо(Х) есть то значение Х, при котором плотность вероятности f(x) достигает своего тах.

Пример 1